みなさんはレバレッジ投信を保有していますか？僕はポートフォリオ内で5%ほど保有しています。手を出したのは最近ですが、驚くほどに大赤字を垂れ流している最中ですw
SNS上でいつも論争の的となっている”レバナス”ことレバレッジNASDAQ100商品、今日もどこかで不毛な議論を続けられていることでしょう。賢い方はそれらを見ないほうがいいと思います。双方ともに言い合ってるだけで、全く生産的ではありません。万が一まともなことを言っているとしてもムダです。相手に聞く耳がない状態で叫んでも意味ないのは明白でしょう。
このブログではそのような論争からは距離をおいて、極めて客観的にレバナスがどんなものなのか？レバレッジはどれくらいに留めるべきなのか？を考えていきたいと思います。レバナスの好き嫌いに関わらず、定量的で納得感ある分析結果を示し、役に立つ情報を届ける所存です。この記事がそんな人の役に立てばそれ以上にうれしいことはありません。
YouTubeも見てね！
以前の分析「レバレッジは1.8倍で中央値が最大になる」
以前にランダムウォーク理論（幾何ブラウン運動モデル）をかじりたての時に分析したのが上の記事です。この記事では中央値（そのリターンを上回る人が50%になる値）はレバレッジ1.8倍付近になると述べていました。左右対称ではない分布においては中央値が一般的に言う期待値的な意味を有してると考えていたからです（※厳密には期待値とは異なるのでご注意）。
ただ、最近統計に対する理解が深まり、これだけでは短絡的であると思うようになりました。それは中央値が同じでも全く異なる特性になりうるということです。
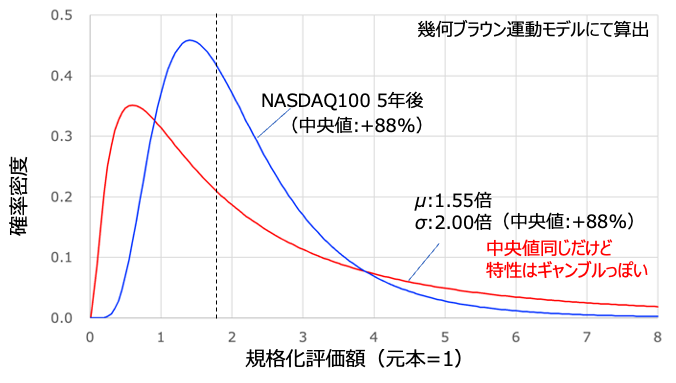
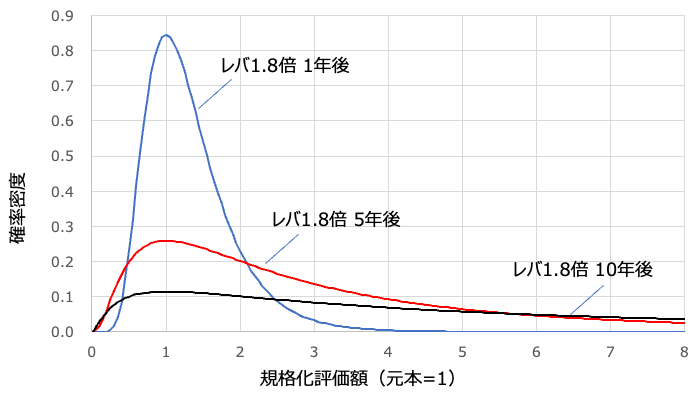
上のグラフはNASDAQ100の5年後の確率密度分布と、それと中央値が同じになるようにイジったものをプロットしています。横軸は規格化評価額で1だと元本と同じ、1より大きいと儲かっているという意味です。
2つのデータは中央値が同じなのに、特性は全然異なるのがわかるかと思います。NASDAQ100は分布のピークが1よりも右にあり、分布が全体的に右に偏っていますよね。これは儲かる人が多く、損する人は少ないという理想的な投資の挙動です。
一方でイジったものはピークは1よりも小さくなっていて、大儲けする人が増えているのがわかります。つまりは大儲けか大損かの2極化が顕著に出ている分布になっているのです。平たくいえばギャンブルっぽい特性と言っていいでしょう。
これらは同じ中央値なのにこんなに特性が異なるのです。だから中央値だけで議論するのは危険かもしれない、と僕は最近考え始めました。
前提：使用するデータの考え方
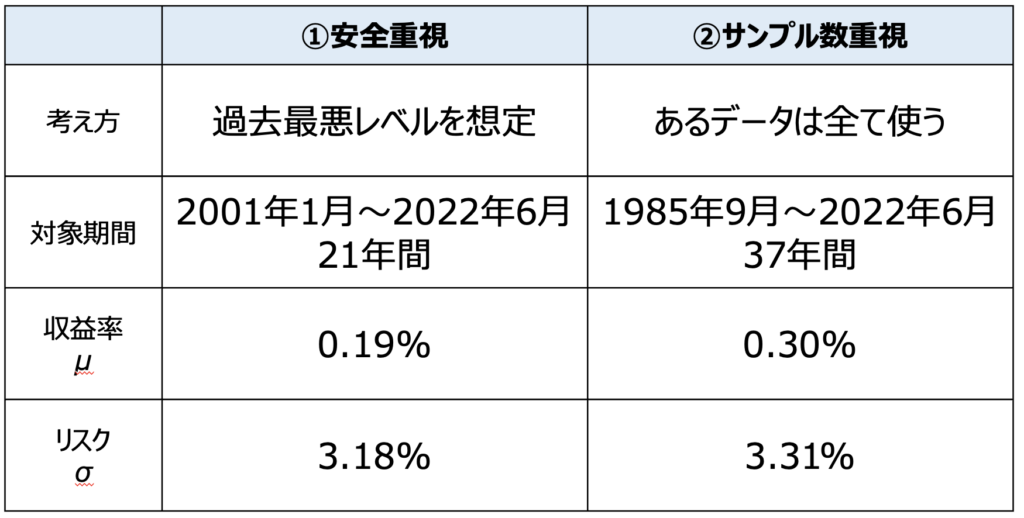
ここからレバレッジが確率密度分布にどのように影響を与えるかを考察していきます。そこで重要になるのが使用するデータです。
今回は２つの考え方で分析を進めます。１つ目は過去最悪レベルを想定して、悲観的な予測をするものです。最悪でも○○だから、こうしとけばいいだろう、そんな考え方ですね。
もうひとつはサンプルデータが存在する限り全て使うというもの。これは統計値は基本的にサンプルデータが多いほうがノイズが少なくなる、という考え方に基づいています。どっちかと言うと僕はこの考え方が好きかな。
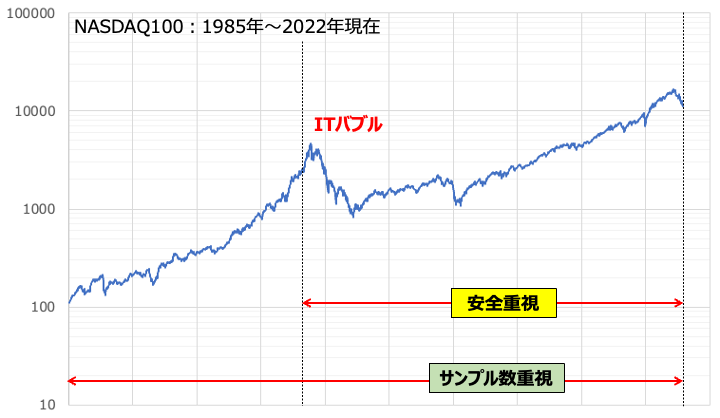
データ使用範囲を明示すると上図のようになります。安全重視はけっこう悲観的で厳し目の計算になりそうですよね〜。
以下は双方のデータを明示して、時には比較を交えていきます。どちらのデータを参考にするのかは、みなさんがどのような考え方で投資商品を選ぶか次第です。
レバレッジが確率密度に与える影響
まずはレバレッジをかけたときの基本的な挙動を見ていきましょう。
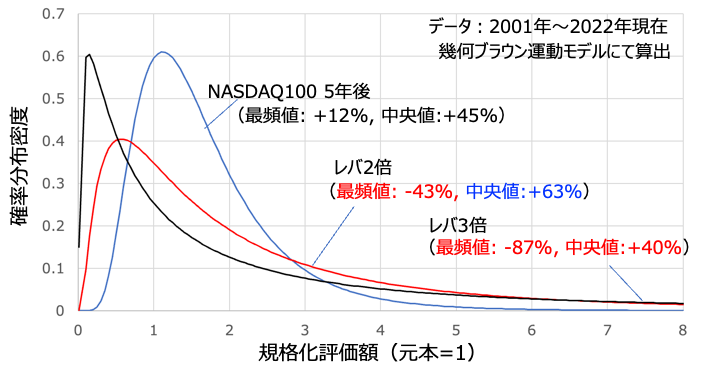
上は安全重視のデータを用いて、レバレッジ倍数を振った時の確率密度分布を示したものです。代表として5年後の分布をプロットしています。
ここからレバ2倍、レバ3倍と倍数を上げていくほど山が左に偏り、右側の裾野が伸びていく様子が見て取れますよね。これはリターンが２極化していることを示していて、一般的にはギャンブル的な挙動が増していると言っていいでしょう。
まあいくらレバナスを盲信しているホルダーの方と言っても、レバレッジが投機性を上げる行為だということは理解しているはずです。これはそれを示しているだけに過ぎません。
一方で気になるのは「長期投資をした時の挙動」です。上の挙動があるからと言って、長期投資に向かないというわけではないので。
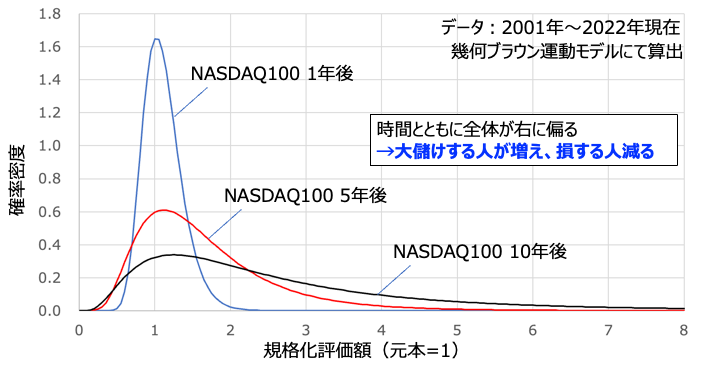
まず上図はレバレッジをかけていないNASDAQ100（安全重視データ）の1年後、5年後、10年後をプロットしたものです。NASDAQ100は悲観的な観測をしたとしても優秀な指数で、時間を経るごとにピークは右に動き、裾野も右に伸びていってます。つまりは長期でやればやるほど大儲けする人が増えて、損する人も減っているのです。まさに理想ですよね。
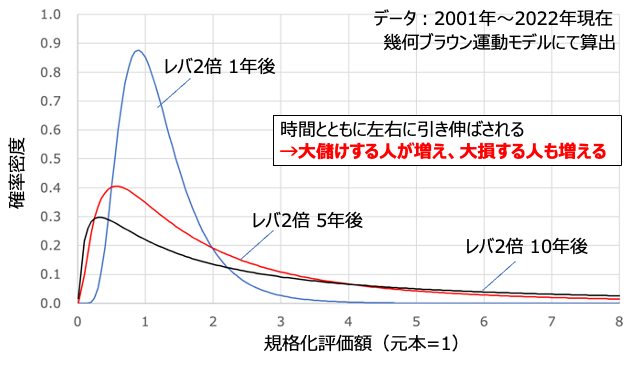
一方でレバレッジ2倍をかけたものが上のグラフになります。先程のレバ無しとは少し挙動が違いますよね。裾野が右に伸びていくのはいいのですが、ピークが左に移動していっているのがわかるかと思います。これは時間とともに大儲けする人が増え、大損する人も増えているという意味です。まあ平たく言うと時間とともにギャンブル化していってるというわけ。ただ、以前の主張通り中央値は上昇しています。これをどう捉えるか次第ですが、このままでは長期投資の最大のメリットである「みんな幸せになれる」には到達しなさそうです。
ギャンブル化させないためのレバレッジ倍数を考える
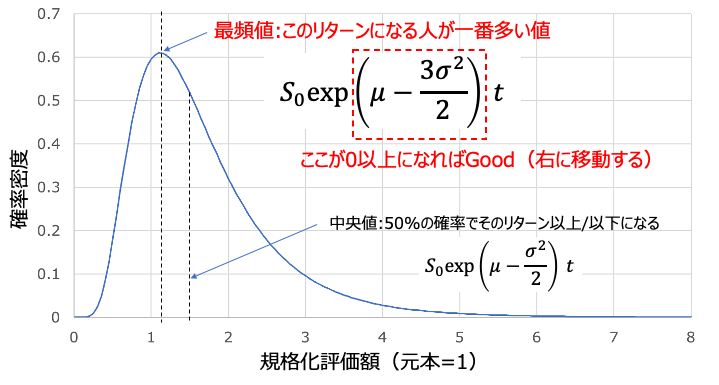
ここまでの分析は特に断ってはいませんが、幾何ブラウン運動モデルを使って確率密度分布を算出したものです。この場合、結果は対数正規分布と呼ばれる分布で表されるため、中央値や最頻値、期待値や平均などの統計数は簡単に計算できます。
上で述べたレバレッジの問題点（というか気持ち悪いところ）は「時間とともに山のピークが左に寄っていく」ことでした。言い換えれば、最頻値が下がっていってるのが問題です。最頻値は上図のように式で表現されるため、指数関数のカッコ内がプラスになっていれば時間とともに山のピークは左に行かないのがわかります。
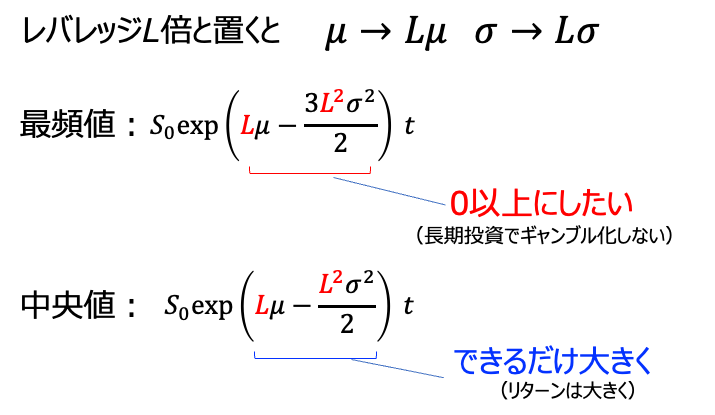
レバレッジをL倍とおけば、最頻値と中央値は上のように表現されます。ここでS0は株価の初期値、tは時間です。特に気にしなくてOK。
この指数関数の中身（二次関数）だけを取り出してプロットしたのが以下のグラフです。
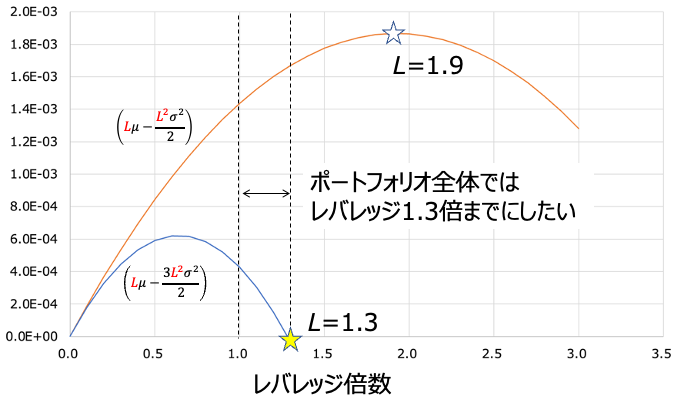
データは安全重視のものを使用しています。ここから、最頻値はレバレッジを1以上かける場合はどうやっても良い方向にはいきません。頂点がレバレッジ1以下のポイントにあり、1以上の領域は右肩下がりにならざるを得ないので。これがレバレッジはどうやっても投機的になるという最も納得いく説明ではないでしょうか？
一方で中央値はレバレッジ1.9倍まで上がり続けるので、できるだけレバレッジをかけたいところではあります。この辺は考え方次第ではあるのですが、僕なら最頻値が0になるポイントである1.3倍くらいを上限にするのがいいかな。つまりはレバナスはサテライト投資にとどめておくのがぴったりだと言うことです。
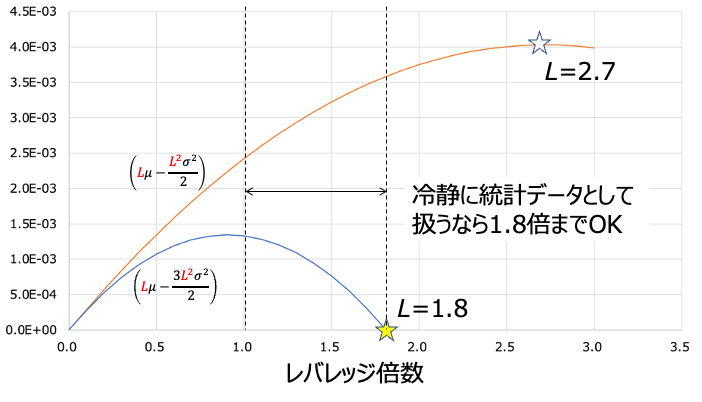
ちなみに使用するデータを「サンプル数重視」にすると上図のようになります。レバレッジ1.8倍までは最頻値も右に動いていくので、意外とレバナスの2倍も悪くなさそうです。だからと言って全力はやりすぎだとは思いますけどね。
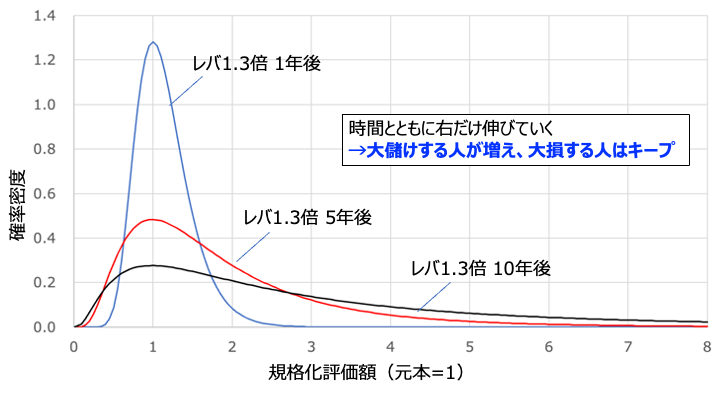
実際に安全重視データにてレバレッジ倍数を1.3にしたデータが上図です。時間とともに右側は裾野が広がって大儲けする人が増えている一方、ピークの位置は動いておらず大損する人も過度に増えていません。これなら長期投資使っても良い特性だと思います。
ついでにサンプル数重視データにてレバレッジ倍数を1.8にしたデータも下に示しておきます。
これを受けての僕の作戦
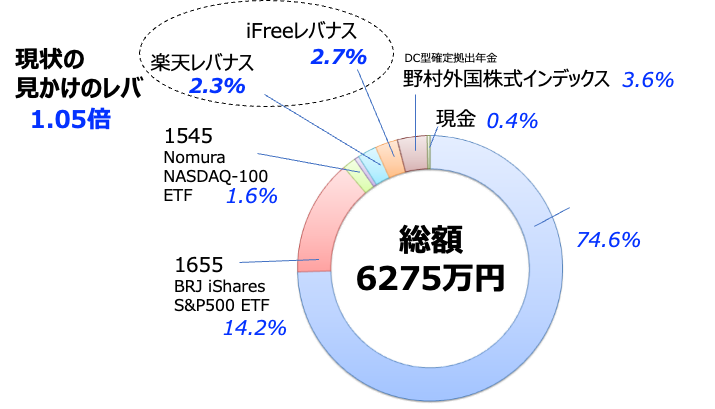
上図は僕の現状のポートフォリオです。最近レバナスを買い進めているものの、買ったそばから下がりまくってるので、比率が大して増えていません。今のところはポートフォリオとして見かけのレバレッジは1.05倍です。1.3倍に収めるためには比率を30%以下にしておけばいいので、まずはそれ以上は買わないようにしておくつもり。
結論：最頻値も意識しながら、自分の考え方でレバ倍数を設計しよう
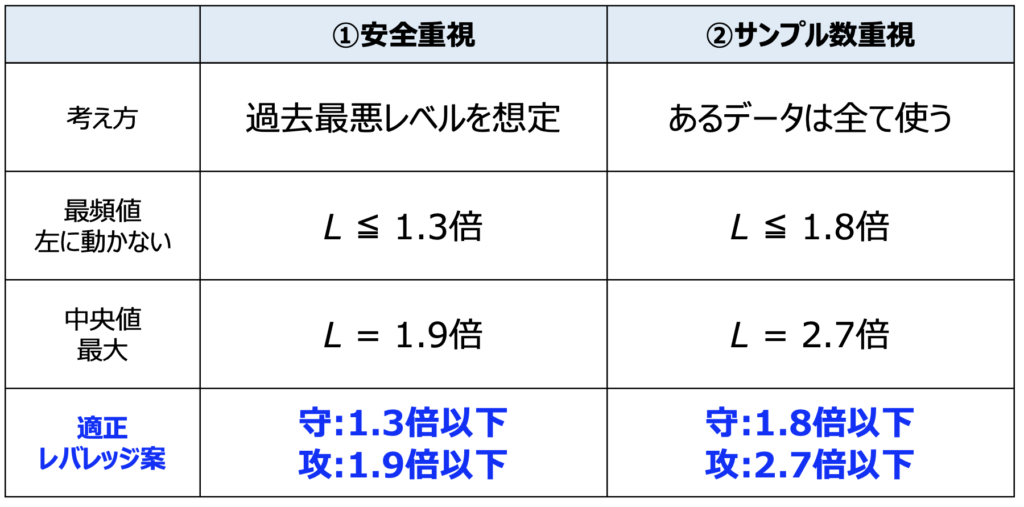
というわけで、以前の検討も踏まえながら整理した結果が上の表です。
まずはご自身が統計分析するとしたらどういうデータを使いたいかを考えて見てください。最悪期でも大丈夫にするのか？それとも、無感情にサンプルとして取り込むのか？分析する目的に沿って選ぶのが普通でしょう。
そうした時に適正レバレッジとして２つの想定を今回考えました。長期投資のよさを引き出すために最頻値が左に動かないように設計する「守り重視」と、あくまで中央値リターンを追い求める「攻め重視」の2つです。それに前述のサンプルデータの考え方をあわせて、パターンは4通りでしょうかね。みなさんの考え方はいかがでしょうか？
僕はデータはサンプル数ある限りとって、最頻値は左に動かないようにしたいかな。なのでレバレッジは1.8倍以下にしたいと思います。まあ現時点でポートフォリオ内の5%しか占めてないから、1.8倍までにはならんでしょうな。
そして最も重要なのは、ここで定義しているμもσも過去の統計値をベースにしていることです。受験で言うと過去問の傾向を分析しているようなもの。傾向をガラッと変えられないという保証はどこにもありません。なので、ここで分析した数値に固執することには何の意味もないと理解してくださいね。あくまで気休めだよ、気休め。
YouTubeも見てね！
投資始めるなら：おすすめの証券会社
-
僕の主力 楽天・プラス・S&P500 や人気の楽天SCHD が買える唯一の証券会社。
-
とにかく視認性がよくて使いやすいのが最大の魅力。
-
楽天プラスシリーズは保有するだけで楽天ポイントもらえる。
- 公式：https://kabu.com/
- au Payカードと組合わせて 1%ポイント還元がアツい。
- 公式サイト：https://www.sbisec.co.jp/
- SBI独自の四半期決算型の高配当投資信託を購入できる唯一の証券会社
- 投資信託で高配当を楽しみたい方はSBI証券が良いでしょう。
投資を学ぶなら：資産運用ですごく勉強になる書籍
僕が実際に読んで「ほんとうに良い本だなぁ〜」としみじみ感じた名著をご紹介します。どれもめちゃくちゃ良い本ばかり。インデックス投資を始めたての方におすすめです。
以下の中にはKindle Unlimited（月々980円 読み放題、初めてだと30日無料キャンペーンもある）のサービスで利用できるものもありますのでチェックしてみてください。
この本は僕が初めて読んだ投資関連の書籍。当時、個別株で失敗し、偶然思うがままに買い付けた米国株インデックスETFに出会い、それにいい感触をもっていました。その感触を自信に変えてくれた本です。僕と同じく、初めて投資書籍を読まれる方にはこの本を最初にオススメします。
投資に関するネット記事は数あれど、最も有名で価値ある記事はコレなのでは？という記事の書籍版です。ぜひ投資書籍の２冊目に読んでほしい一冊としてピックアップしました。これを読むだけで本当に資産運用が完結する内容になっていて、僕も当時衝撃を受けました。もちろん書籍版の内容の本質はネット記事とほぼ同じですが、理論編がわかりやすく改定されていたり、読みやすくなっています。
![敗者のゲーム[原著第8版]](https://m.media-amazon.com/images/I/512Xx-NQJGL._SL160_.jpg)
インデックス投資の名著中の名著です。個人投資家にとっての投資は「ミスった者が負ける」敗者のゲームになった、というのがタイトルの由来。ここで言うミスとは、市場動向に動揺して売買してしまうことを指します。いいからインデックスホールドしとけ、という本。インデックス投資家の教養として読むべき本です。
これは僕が最近読んでよかったと思ってる本です。マクロ経済における金利の重要性を懇切丁寧に説明してくれています。金利が経済の基本であることを再認識させられました。初心者でも読みやすいように書かれていて、とくに予備知識は必要ありません。投資タイミングに活かせるかと言えばそこは同意しかねますが、金利による経済の定性的な動きを理解するのはこれで十分と思いました。
この本はKindle Unlimitedの読み放題サービスで提供されていることが多いです。Kindle Unlimitedは初めてであれば30日無料体験が使えるので、それで読み切ってしまうのもいいかと思います。僕はそうしました。
これは最近複数の視聴者さんに紹介してもらって購入した本です。主張は題名どおり「余剰資金が出たら即刻インデックス投資せよ」というもので、僕も思想とほぼ一致しています。また、前半部分では「節約には限界がある」「収入を増やす努力をしよう」という主張もされていて、その辺も共感できる部分は多いです。とてもいい本だと感じましたので、よかったら手にとってみるとよいかと思います。
これは最近視聴者さんに教えてもらった本です。株式投資や資産運用の考え方を学ぶのに、とても素晴らしい名著だと思いました。著者はインデックス投資にも精通していることが伺える一方で、各個人の資産運用は人としての合理性も考慮すべきと説いてます。株式投資のリターンは「リスク（値動き）の対価」をわかりやすい例も含めて明示してくれていて、投資初心者の方にぜひ読んでみてもらいたい本ですね。
2024年の年初に亡くなられた山崎元さんの遺作。内容は父から息子への手紙をイメージして、資産運用や生き方のアドバイスをおくるというもの（実際に送られた手紙の内容もあります）。涙なしには読み切れない名作でした。投資における主張はいつもの著者のものと全く同じ。ブレないところが山崎さんの良さですね。ぜひ読んでもらいたい一冊。
米国の著名投資家ハワード・マークス氏の著書で、彼の著書はなんとあのウォーレン・バフェットのお気に入りらしいw バークシャー・ハサウェイの株主総会でこの本を配ったというウワサも残っています。ハワード・マークス氏自体はインデックス投資にも一目を置くアクティブ投資家で、市場平均に勝つのは難しいと認めつつもどうすれば勝てるか？を色々とアドバイスしてくれる本です。
僕が一番好きな本。難しい数学的な知識を必要とせず、現代ポートフォリオ理論（≒ランダムウォーク理論）をかじれます。正直な感想を言うと全ての書いてることが興味深かったわけではありません。なので隅々まで読んだわけではないですが、理論のところはとてもわかりやすいのでおすすめです。これ読んでからWikpedia見たらだいぶ理解が進みました。
上記の本に加えてもう少しファイナンスを詳しく知りたい方向けにおすすめです。CAPMの考え方やそれをもう一歩発展させた3ファクターモデルのことも理解できます。ほかにもプライシング理論やリスク管理などの基礎知識もこれで十分わかるかと。
インデックス投資の父でありVanguard創業者のBogle氏の名著です。僕が最も尊敬する偉人でもあります。その先見性と残された功績には尊敬の念しかありません。内容はインデックス投資のベーシックな内容ですが、後半には債券との組み合わせ論などにも言及されています。全部が全部同意見というわけではありませんが、インデックス投資を志す者であれば必読書とも言ってよいかと。
ランダムウォーク理論（株価の動きはわからないという前提を置く理論）について、歴史を交えて語った本。これも名著と言われています。理論の概念はざっくりとわかるかと。歴史の部分が長くて、そこは読み飛ばしました。
本をほとんど読まない僕が唯一知ってる作家さん、橘玲さんの本。とても読みやすい文章で書かれていて、こんな文が書きたいなといつも思ってます。僕が海外株を中心に買っているのはこの本の考え方に近いです。
かつて日本の長者番付で一位になったサラリーマンとして話題になった清原達郎氏の初めての著書。これまでメディアにほとんど出てこなかった氏の赤裸々な体験談が多数載せられています。内容は初心者向けではありませんが、どこにでも溢れているインデックス投資を勧めるだけの本に飽きた方にはとても面白いはず。かく言う私もその一人（笑）純粋な読み物としてとても面白いです。
社会保険料がホットな話題として挙げられることが増えました。本書はその社会保険料の節約として最も有名な「マイクロ法人スキーム」のきっかけになった名著です。いま巷で使われているマイクロ法人という言葉は、この書籍で初めて使われたと言われています。もしマイクロ法人設立に興味があれば、まずは最初のバイブルとして読破しておくべき一冊です。
※以下のリンク先におすすめ書籍をまとめています
