※22年11月追記：以下の検討はレバレッジ投信特有の”短期金利の影響”を考慮できていません。近日中にこれを考慮した記事をアップしました。→こちら
みなさん、最近の下落相場をいかがお過ごしでしょうか？何回経験しても下落相場というのは嫌な気持ちになりますよね。ぼくなんてキャッシュをほぼ持ち合わせておらず余計に気持ち悪いですw 身動きごれませんから。
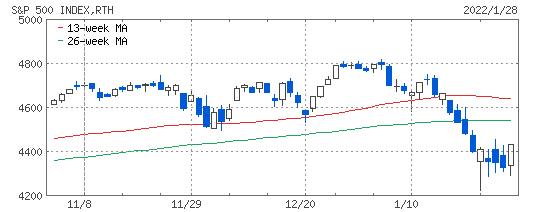
しかしチャートを見るとそろそろ底かな〜という雰囲気を醸し出しております。こういうときに投入したいのがレバレッジ投信ではないでしょうか？いわゆるインデックスの値動きに倍数をかけた攻めの商品です。
このレバレッジ商品は最近論争の的になっています。確かにボラリティが高いので少し投機的な側面があるのは否めません。けれども所詮は変化率に倍数をかけただけのものです。どこかに最適な点があってもおかしくありません。そんなことを考えていたときに、Twitterでこんな投稿を見かけました。
どうやら最適レバレッジを考察する統計的な手法があるようです。ただ、残念ながらこの投稿を読むだけでは僕の脳みそでは理解できません。
というわけでこの数式をたどって自分なりに上記の考え方を辿ることにしました。僕は統計学は全くの素人です。そのため以下に示す計算は間違っている可能性が多いにありますのでご注意ください。それよりも”自分で計算するんだ”という気概を見せるためにこの記事を投稿したいと思います。この記事が誰かの役に立てばそれ以上にうれしいことはありません。
賢い人が考えた株価の表現：幾何ブラウン運動モデル
いきなり数式で驚かせてすみません。どうやら世の中の賢い人たちは株価を”幾何ブラウン運動”というモデルで記述するとよく合うと言っているようです。上の式がそれ。ぱっと見るとびっくりしてしまいますが、考え方はそんなに難しくありません。
まず左辺 dS は株価の変化です。これは 今日の株価 – 昨日の株価 みたいなイメージですね。
その dS を2つの足し算で表現できると言っているのです。１つ目 μSdt は株価が少しずつ上昇していく成長率のこと。S&P500なら年平均8%とか言ったりしますよね。それ効果を表す部分のこと。算術平均リターンと言います。
もうひとつのσSdz はランダムに動く項です。株価ってランダムに動くじゃないですか。それを表現しているわけです。σはそのばらつきの大きさ（ボラティリティ）、dz はノイズ。ノイズは正規分布するとみなします（正規分布：身長やテストの点数などのランダムな分布のこと）。株価変化の標準偏差で定義します。
これを見ただけじゃイメージ湧かないなぁ・・・
というのでイメージに起こすとこんな感じです。(参照サイト）
とりあえず株価の対数をYとおいてグラフにしています。Yは平均成長率で少しずつ右肩上がりに沿いながら、各時刻ではランダムに動くようなイメージです。そのため、株価はギザギザ動きながら右肩上がりに推移していきます。たしかにそんな動きしてますよね〜。
注意すべきはこれが株価の対数の動きであることです。株価の対数が正規分布しているので、これを対数正規分布と呼ぶらしい。よくわからないので詳しい説明はWikipediaに任せます。
実際にS&P500の株価と比べたらどうなん？
いろいろと屁理屈をこねるのは結構なのですが、そのモデルが実際の株価をうまく表現できていなかったら意味がありません。というわけで実際に1985年〜2022年のS&P500の日毎データで比較してみた結果がこちら。
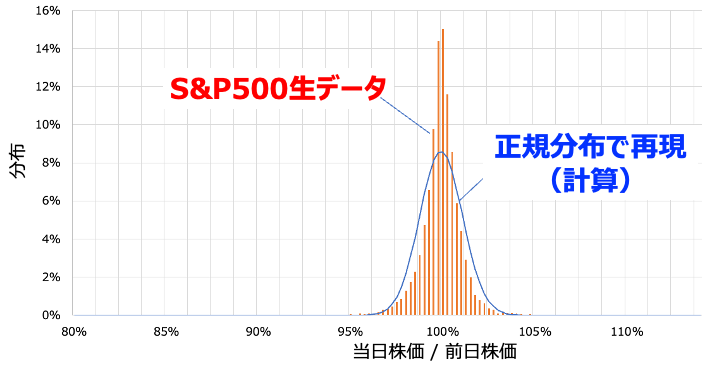
青い線が計算、ヒストグラムが実際のデータです。うーん、これで表現できていると言っていいのでしょうか？微妙な気分ではありますが、他の人が計算した例なども見てみたかぎりはこんな感じの例が多かったです。検算はかなりしたので計算ミスは無いと思っていますが・・・。まあモデルとはこんなものですかね。もっと難しいモデルを提唱している人も海外にはいるみたいでした。それは解読不能。
とりあえずここでは株価は幾何ブラウン運動で表現できているという前提で話を進めます。
期待リターンはどう考えるのか？
対数正規分布は大げさに描くと上図のように左右非対称な形になっています。そうすると平均値と中央値の意味が変わってくるのです。平均値は一番理解しやすい数値ではありますが、こういう分布の場合は全体よりもやや右よりに引っ張られがちになります。これは凄くリターンを得られた一部の人が平均値を引っ張ってしまうからです。
一方の中央値はちょうど真ん中の順位のイメージです。中央値を上回る確率は50%、それ以下の確率も50%になるような値ですね。こういう非対称な分布の場合は中央値を使うほうが実感に合いやすいでしょう。というわけで中央値で考えてみます。
幾何ブラウン運動の中央値はどう計算する？
ぼくはここで理解に躓き、数時間格闘しましたw その苦労の果てに理解できたことは以下のとおりです。
対数正規分布の中央値は公式があります。中央値 = exp(μ0) です。ここのμ0は幾何ブラウン運動のμとは異なることに注意してください。これはあくまで対数正規分布の平均値です。
一方で幾何ブラウン運動のWikipediaには以下の記載があります。
統計的性質
幾何ブラウン運動の確率変数 log(St /S0) は、平均(μ-σ2/2)t 分散 σ2t の正規分布にしたがい、その平均と分散は以下のように表せる。
つまりは対数正規分布のμ0に幾何ブラウン運動の平均値を代入すればOKなのです。つまり、幾何ブラウン運動の中央値は
中央値 = exp(μ-σ^2/2)t と表されるわけです。これに気づくのに数時間かかりました・・・w
そうするとレバレッジをかけた中央値はこう表現できます（以下は初期値をY0としてます）
これで準備は整いました。レバレッジの効果を考えるには レバありの中央値/普通の中央値 を考えればよいのです。いわゆる比です。それを計算したのが以下。
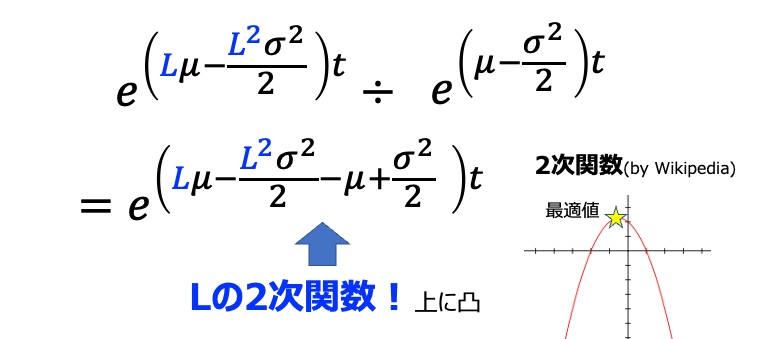
上のeの肩にある式がLの2次関数になっています。μとσは定数ですし、tは時刻なので正の数です。つまりはレバレッジ倍数の最適値はLの2次関数の最大値問題に帰着します。ここまでくれば高校１年の数学です。僕でも解けます。
というわけでこれをS&P500で分析した結果がこちら。（※追記：2022年11月差し替え）
これで見るとS&P500の中央値が最大となるレバレッジは3.1倍あたりとわかります。つまり3倍以上かけるのはそれこそ博打です。上昇局面の極めて短期間にとどめておくのがよいでしょう。
※他のブログなども調査したのですが、一般的には最適値1.75倍程度としている人が多いようです。可能なかぎり検算をしてますが、ぼくの計算は間違っている可能性があるので信用しないでください。レバレッジのかけ過ぎは止めとけ、くらいの認識でいてくれるとうれしいです。
同じくNASDAQ100で計算してみた結果がこちら。（※追記：2022年11月差し替え）
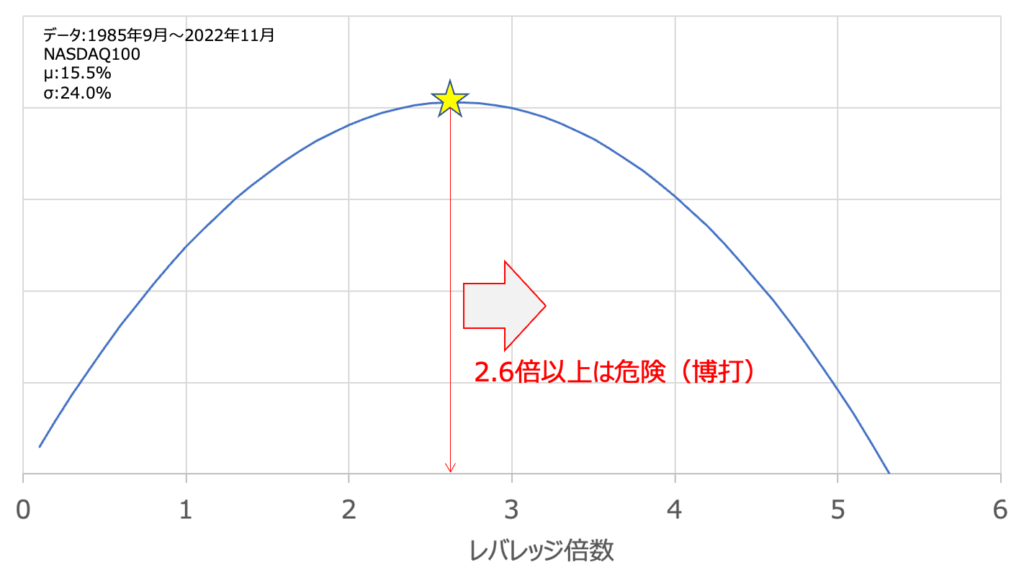
NASDAQ100はボラリティがS&P500より高いため、レバレッジ倍数に耐性が強くありません。なので2.6倍程度のところで中央値最大をとり、急激に下がっていく傾向がわかります。この約2倍という数値はTwitterのゆいさんが述べられていた結果より少し大きめでした。詳細はわかりませんが、たぶん参照してる期間が違うんじゃないかな？と思ってます。
ギリギリ攻めるならどうやって買う？
S&P500であれば2倍投信や3倍投信が販売されていますので、1557や1655などの普通の連動商品とミックスすればよいと思います。ミックス具合はどれくらい攻めたいかで設計してください。
NASDAQ100はレバナスがちょうどいい商品です。本当はQLDがベストなんですが楽天証券で買えないんですよね〜。為替ヘッジがいらん。2倍ギリギリを攻める必要もないので、倍率を下げる場合は1545などを混ぜるとよいでしょう。
リバランスしなきゃいけないかって？厳密性を求めるならそうでしょうが、ここまでの議論にそのような厳密さはありません。所詮確率で述べてるだけです。適当に順次買い付けする銘柄を調整してリバランスっぽいことしとけばいいと思ってます。リバランスと称して売買してたら、その分の税金がもったいないよ、たぶん。
レバレッジ物を推奨しているわけではないので注意
今の下落相場で実感している人が多いと思いますが、レバレッジ物のストレスは半端じゃないです。上の分析を理解したからと言ってリスク許容度を無視して買うと精神が崩壊します。以下は平常時と暴落時の下落幅を計算したものです。
1400万円全力投資するとこれくらい動くのを理解しておかねばなりません。いくら最適値をねらったと息巻いていたとしても精神がやられて退場しては意味がないのです。Stay in Market を守れるレバレッジ倍率設計が一番重要ですね。
結論：いちばん言いたいのは脱！思考停止
上の検討は素人の僕が計算したものなので、間違いがあるかもしれません。それでも、自分で考えるということは生きていく上で非常に重要だと思うのです。
残念ながら巷では
レバレッジ物はカスだ！絶対に長期投資に使ってはいけない！
という声をそのまま鵜呑みにして信じてしまっている人が多くいるらしいです。まともな数字感覚をもっていればそうではないことはすぐに気づくはずです。というのもレバレッジというのはベース指数の変化率に定数を乗じただけのものですから。
そのため「レバレッジ=悪」 という思考は間違いで、正しくは「レバレッジのかけ過ぎ＝悪」というのが本来のはずです。上の例だと2倍あたりがしきい値になります。
例えば1.00001倍のレバレッジもダメなのか？と考えさえすれば、変な煽りを信じ込むことはないと思うのですが・・・自分で考える習慣をなくしてはいけないとつくづく思います。
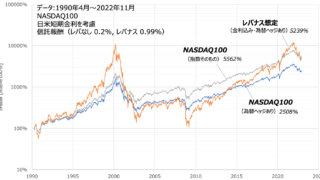
追記：レバレッジ投信への金利の影響を考慮しました
追記：中央値だけで”最適”と言うのは言い過ぎかな〜と再考しました
おまけ：資産運用おすすめ書籍
僕が実際に読んで「ほんとうに良い本だなぁ〜」としみじみ感じた名著をご紹介します。どれもめちゃくちゃ良い本ばかり。インデックス投資を始めたての方におすすめです。
以下の中にはKindle Unlimited（月々980円 読み放題）のサービスで利用できるものもありますのでチェックしてみてください。Kindle Unlimitedは無料期間もたまにあります、いつかはわからないけど。
2024年の年初に亡くなられた山崎元さんの遺作。内容は父から息子への手紙をイメージして、資産運用や生き方のアドバイスをおくるというもの（実際に送られた手紙の内容もあります）。涙なしには読み切れない名作でした。投資における主張はいつもの著者のものと全く同じ。ブレないところが山崎さんの良さですね。ぜひ読んでもらいたい一冊。
かつて日本の長者番付で一位になったサラリーマンとして話題になった清原達郎氏の初めての著書。これまでメディアにほとんど出てこなかった氏の赤裸々な体験談が多数載せられています。内容は初心者向けではありませんが、どこにでも溢れているインデックス投資を勧めるだけの本に飽きた方にはとても面白いはず。かく言う私もその一人（笑）純粋な読み物としてとても面白いです。
これは最近複数の視聴者さんに紹介してもらって購入した本です。主張は題名どおり「余剰資金が出たら即刻インデックス投資せよ」というもので、僕も思想とほぼ一致しています。また、前半部分では「節約には限界がある」「収入を増やす努力をしよう」という主張もされていて、その辺も共感できる部分は多いです。とてもいい本だと感じましたので、よかったら手にとってみるとよいかと思います。
これは最近視聴者さんに教えてもらった本です。株式投資や資産運用の考え方を学ぶのに、とても素晴らしい名著だと思いました。著者はインデックス投資にも精通していることが伺える一方で、各個人の資産運用は人としての合理性も考慮すべきと説いてます。株式投資のリターンは「リスク（値動き）の対価」をわかりやすい例も含めて明示してくれていて、投資初心者の方にぜひ読んでみてもらいたい本ですね。
これは僕が最近読んでよかったと思ってる本です。マクロ経済における金利の重要性を懇切丁寧に説明してくれています。金利が経済の基本であることを再認識させられました。初心者でも読みやすいように書かれていて、とくに予備知識は必要ありません。投資タイミングに活かせるかと言えばそこは同意しかねますが、金利による経済の定性的な動きを理解するのはこれで十分と思いました。
米国の著名投資家ハワード・マークス氏の著書で、彼の著書はなんとあのウォーレン・バフェットのお気に入りらしいw バークシャー・ハサウェイの株主総会でこの本を配ったというウワサも残っています。ハワード・マークス氏自体はインデックス投資にも一目を置くアクティブ投資家で、市場平均に勝つのは難しいと認めつつもどうすれば勝てるか？を色々とアドバイスしてくれる本です。
僕が一番好きな本。難しい数学的な知識を必要とせず、現代ポートフォリオ理論（≒ランダムウォーク理論）をかじれます。正直な感想を言うと全ての書いてることが興味深かったわけではありません。なので隅々まで読んだわけではないですが、理論のところはとてもわかりやすいのでおすすめです。これ読んでからWikpedia見たらだいぶ理解が進みました。
上記の本に加えてもう少しファイナンスを詳しく知りたい方向けにおすすめです。CAPMの考え方やそれをもう一歩発展させた3ファクターモデルのことも理解できます。ほかにもプライシング理論やリスク管理などの基礎知識もこれで十分わかるかと。
![敗者のゲーム[原著第8版]](https://m.media-amazon.com/images/I/512Xx-NQJGL._SL160_.jpg)
インデックス投資の名著中の名著です。個人投資家にとっての投資は「ミスった者が負ける」敗者のゲームになった、というのがタイトルの由来。ここで言うミスとは、市場動向に動揺して売買してしまうことを指します。いいからインデックスホールドしとけ、という本。
インデックス投資の父でありVanguard創業者のBogle氏の名著です。僕が最も尊敬する偉人でもあります。その先見性と残された功績には尊敬の念しかありません。内容はインデックス投資のベーシックな内容ですが、後半には債券との組み合わせ論などにも言及されています。全部が全部同意見というわけではありませんが、インデックス投資を志す者であれば必読書とも言ってよいかと。
ランダムウォーク理論（株価の動きはわからないという前提を置く理論）について、歴史を交えて語った本。これも名著と言われています。理論の概念はざっくりとわかるかと。歴史の部分が長くて、そこは読み飛ばしました。
本をほとんど読まない僕が唯一知ってる作家さん、橘玲さんの本。とても読みやすい文章で書かれていて、こんな文が書きたいなといつも思ってます。僕が海外株を中心に買っているのはこの本の考え方に近いです。
この本は僕が初めて読んだ投資関連の書籍。当時、個別株で失敗し、偶然思うがままに買い付けた米国株インデックスETFに出会い、それにいい感触をもっていました。その感触を自信に変えてくれた本です。
※以下のリンク先におすすめ書籍をまとめています
