みなさん、巷にあふれているインフルエンサーの株価予想動画を見るのは好きですか?自分で投資動画あげておいてアレなんですが、僕は正直ほとんど見ていません。なぜなら僕は株価は何かしらのアノマリーを持って動いているとは思うものの、それを予測することは困難で時間の無駄だと考えているからです。
僕のような考え方をする人がやる投資法はインデックス投資です。時価総額加重平均で投資すればシャープレシオがベストに近くなる、というCAPM理論(※古い理論)に共感する人たちですね。このような人たちのうち多くの人はお金というものの執着心から解かれた、悟りの境地に達したような人も多くいます。僕もそんな存在になりたい、そう思って修行に励む日々です。
いわゆる「ランダムウォーク理論」支持者としては、株価予想をすることはできません。一方で、ランダムに動くと仮定すれば、将来の株価がどのように分布するかを記述できるのは知っていました。今回は他のインフルエンサーがやらなさそうな、リターンとリスクを考慮したS&P500のガチ株価予想にチャレンジしてみようと思います。この記事が、これから投資を始める方の参考になれば、それ以上にうれしいことはありません。
YouTubeも見てね!
よくある株価予想の例

最も多いのは「過去のデータと同じ動きをする」という例です。たとえは上図のようにある一定期間を切り出し、特定の指数が優れていると主張します。そして、あろうことか差が今後も続くかのように言う人もいるくらいです。
こういう予想は製作者側に立つととても簡単にできるので都合がいいんです。そして視聴者さんにとってもわかりやすい。過去にあったことなら、未来にも起こる。説得力ありますもんね。
ただ当たり前ですが、過去と全く同一のことは二度と起こりません。入試でも同じ過去問が出ることはないでしょ。それと同じだよ。
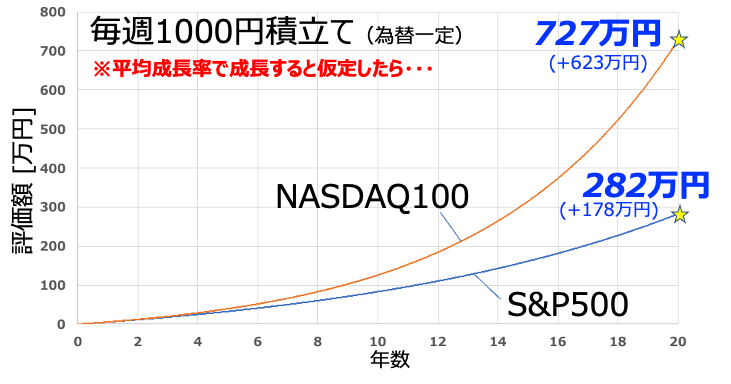
もうひとつは統計処理をするものの、その平均成長率だけを使って株価予想するものです。これは僕も過去にたくさんやってきてます、すみません・・・orz。この予想もそんなに褒められたものではありません。それは統計値のもうひとつの重要なデータ、リスク(変動)が考慮されていないからです。
リスクを考慮しないとどうなるか?
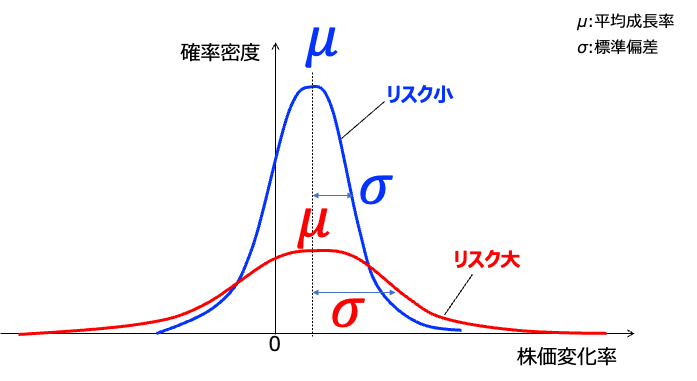
例えば上図のようなμ:平均成長率は同じだけど、σ:リスク(標準偏差)が異なるものがあったとします。当然赤線のリスクが大きいほうが将来の株価はばらつきますし、レバレッジ投信で有名な逓減を喰らうことだってあるでしょう。そういう懸念がμだけで表現すると織り込まれていないんですよね。
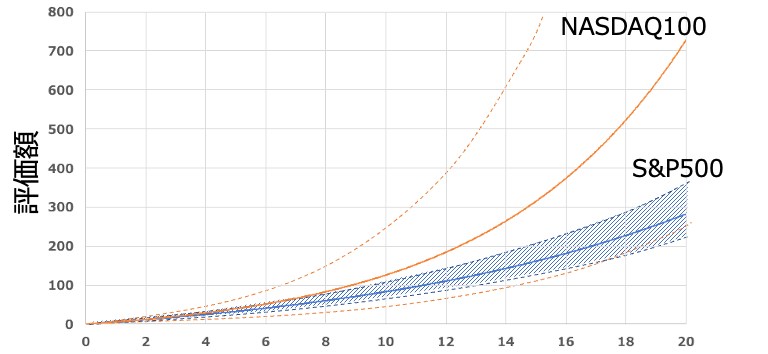
上図はばらつきの影響を絵でわかりやすくイメージしたものです(値は正確なものではありませんのでご注意)。例えばNASDAQ100がS&P500よりもめちゃくちゃσが大きかったとしたら、将来の結果は大きくばらつき、S&P500を下回ることも多くなるはずです。これらの事象がリスクを考慮しない計算では全く見えません。
幾何ブラウン運動モデルで株価予想をしてみる

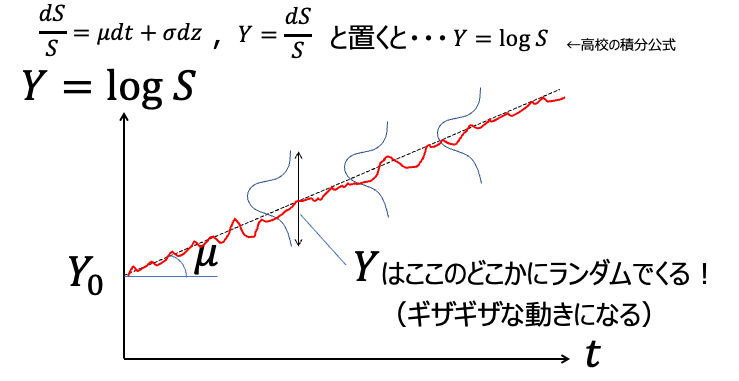
本ブログおよびYouTubeでもたびたび使っている、この幾何ブラウン運動モデルを導入して計算してみることにします。この式は難しそうに見えますが考え方は簡単です。時間とともに少しずつ成長する第一項とランダムに動く第二項を足し合わせたものが未来の株価だと言ってるに過ぎません。
難しい途中式の展開はWikipediaに任せるとして、この式から株価は対数正規分布として表現できるという結論が導かれます。イメージは以下のような感じ。
対数正規分布を使って予想する1年後のS&P500

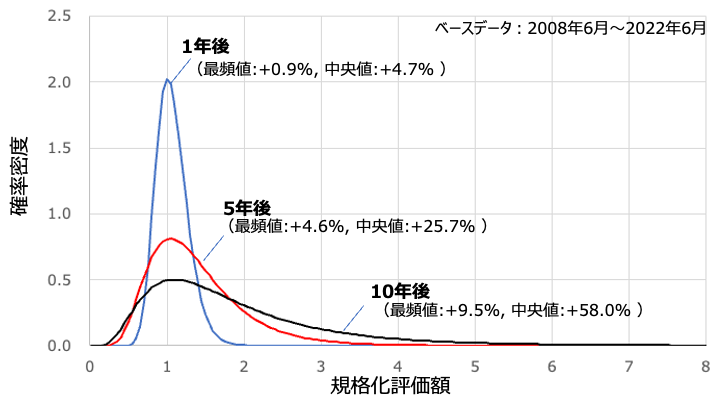
というわけで早速結果を見ていきましょう。上図は1年後のS&P500の値を予想したものです。ベースデータは1970年1月〜2022年6月のものを使っています。
横軸は規格化評価額で1だと全く成長していない、という意味です。この結果を見ると僅かに右側に偏っているのがわかるかと思います。これはS&P500が成長する可能性が高い、ということを示したもの。
注釈の中にある最頻値とは文字通りこの分布で最も多いポイントを指します。頂点ですね。イメージで言うと1000通りのパラレルワールドがあったとして、最も多いワールドが+4.7%だったということです。
一方で中央値とはちょうど真ん中の順位のことを指します。1000通りのパラレルワールドのうち、リターンの大きさが500番目になる世界のリターンです。
どちらを重視して見るかは各個人の判断だとは思いますが、僕のイメージは中央値は期待リターン的なもので、最頻値は危険性を表現するような捉え方をしています。μとσの組み合わせによっては、最頻値が低く中央値が高い場合もあり得るのです。理想的には最頻値と中央値がともに右よりに分布するのが良い商品と言えます。
なお、一般的に統計値として有名な平均値や期待値はこのように偏った分布の場合は意味が薄いです。めちゃくちゃ儲かったやつがだいぶ引っ張ってしまうので。
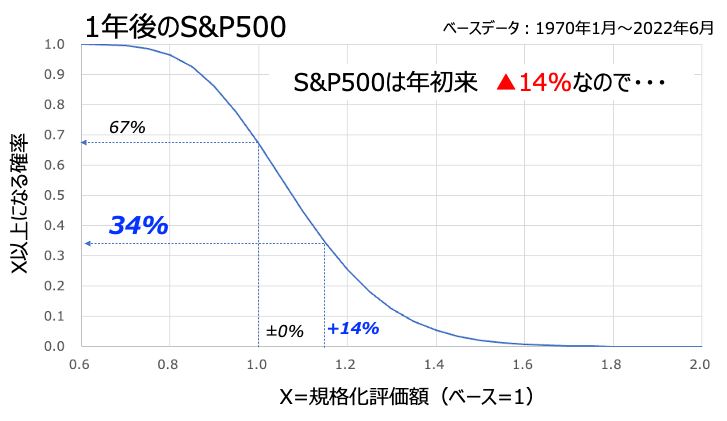
ついでにこの確率密度分布を積算すれば、確率を求めることができます。上の図は1年後のS&P500が横軸X以上になる確率を計算したものです。全体的に右に偏った分布から想像されるとおり、±0%以上になる確率は50%を超えて67%にまで達するのがわかります。そして年初から14%下落したS&P500が1年後に回復する確率も34%と具体的な値で算出することができるのです。カンタンなのになかなか面白いですよね。
この予想から長期投資のパワーがわかる
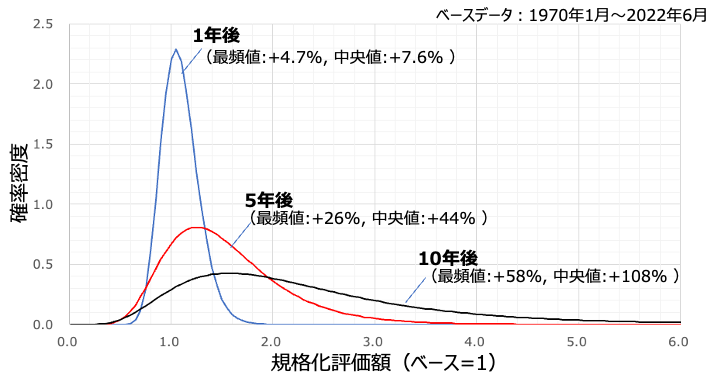
続いてS&P500に対して時間をパラメータに分布を調べてみましょう。上図は5年後、10年後を追加プロットしたものです。一見してわかるとおり、年数を経るごとに分布が右に偏っているのがわかるかと思います。最頻値、中央値ともに右に移動しているということは、つまりは誰しもが儲かるようになっている、ということです。これが長期投資の力ですよね。
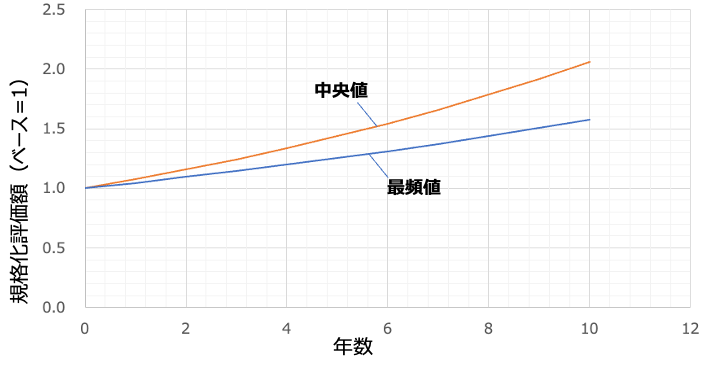
実際に年数を横軸にして中央値と最頻値をプロットしてみたのが上図です。どちらも単調増加していて、長期で運用するということは良いことしかない、というのを結果が表しています。
リスクσと収益率μはどのように影響するか?
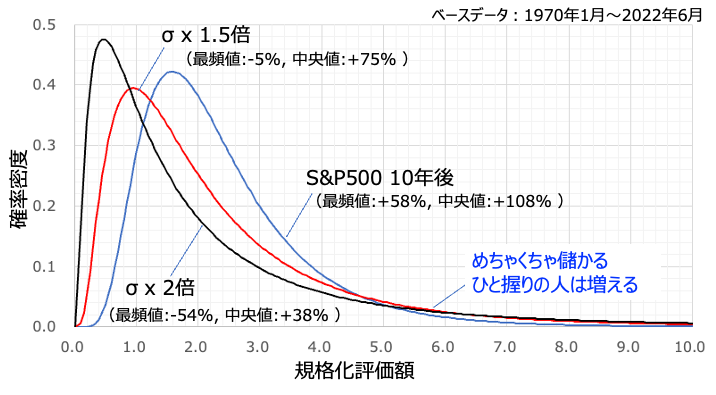
最も興味が湧くのはリスクの影響です。なにせほとんどの発信者が言及していないところですから。上図はS&P500 10年後に対して、リスクを1.5倍、2倍にしたものをプロットしています。
結果を見てまず目につくのは山が左に寄っているところでしょう。最頻値は下がってしまっていて、10年後でもマイナスです。1000人に聞いたらマイナスだと答える人が多いということ。10年もかけたのに・・・。そして中央値ももちろん低下していきます。これは逓減のせいですね。
一方でグラフの右端に目を向けると逆転するポイントがあることに気づきます。これはリスクが大きい商品はめちゃくちゃ儲かる人ひと握りの人が多くなる、という結果です。上の最頻値の傾向と合わせて考えると、分布が左右に引き伸ばされて二極化していると言っていいでしょう。つまりはギャンブルになっている、というわけです。
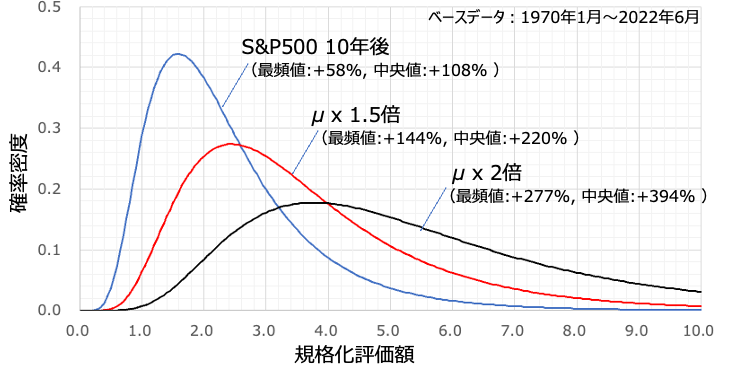
一方の収益率をパラメータにすると上のような分布になります。これは想像どおりと言っていい結果ではないでしょうか?収益率が上がると最頻値も中央値も右に偏っていきます。いいことしか起こっておりません。めちゃくちゃ儲かる人が逆転するようなポイントもないですね。
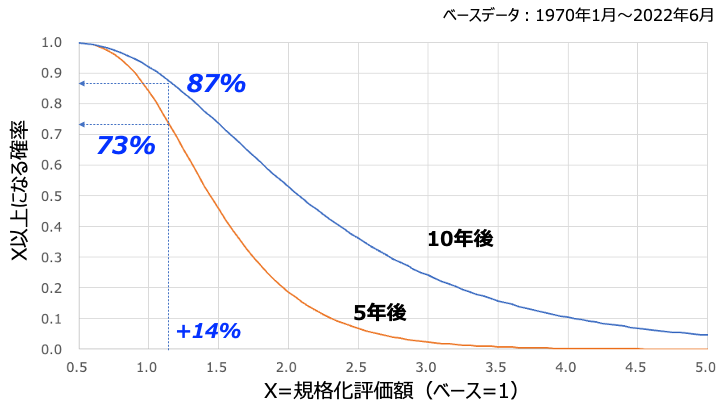
ついでに長期投資した場合に現在のS&P500下げ幅▲14%をどれくらいの確率で回復するかも計算してみました。前述の1年の場合だと34%の確率だったわけですから、かなりの高確率になっているのがわかりますよね。これが長期投資の真の実力です。まあ当然、クソみたいな商品を長期投資で持っていてもクソのままなので、無条件で長期投資が凄いわけではないのはご留意ください。
ついでに別の指数も調べてみよう
みなさんが興味あるのはS&P500ではないかもしれません。ついでにNASDAQ100とオルカン(≒VT)も調べておきました。前提は以下のとおり。

統計データなのでできるだけ対象期間は長くとりたいものです。VTの歴史が浅いので悩んだ末に、各指数で最も長い期間で分析をしました。期間が同一でないので、フェアな比較ではないことを予めご了承ください。

上図は10年後の各指数の計算結果です。まあ想像のとおりだとは思いますが、過去のNASDAQ100は最強なので、ここでも無双の力を見せつけました。分布がきれいに右に寄っていますよね。まあS&P500もVTも十分優秀だとは思います。
参考:NASDAQ100の詳細計算

参考:VTの詳細計算
この知識をどう使うのか?
ここまでごちゃごちゃと言ってきましたが、最終的に言いたいのは「リターン(夢)だけに目をとられるな」ということです。リターンが同じでもリスクが異なれば結果は全く違うものになるのです。
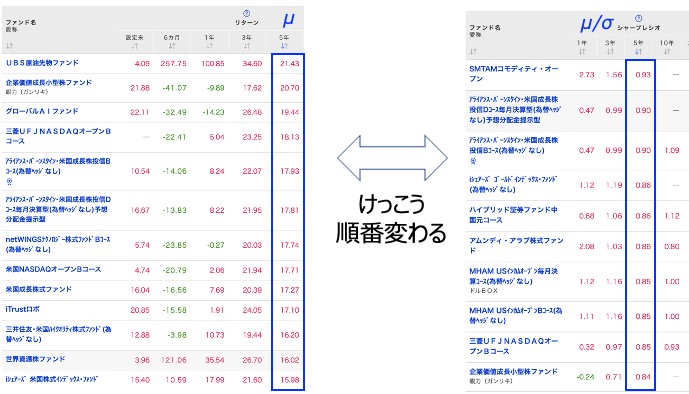
例えば楽天証券の投信スーパーサーチというシステムではリターンの他に標準偏差やシャープレシオを見ることができます。標準偏差はめちゃくちゃ小さいものが存在してしまってよくわからなくなるので、シャープレシオを見てみるのがよいかと。下図は5年リターンと5年シャープレシオをランキングにしたものですが、けっこう順番が変わるのがわかりますよね。リターンとシャープレシオの2面で投信を評価すると十分活用できていると思いますよ。
まあそもそも10年しか分析できないし、それに10年続いている投信も少ないし、どこまで使えるかどうかはアレですが・・・。
結論:リターンだけ見てたら痛い目に遭うよ
株式投資のいちばんわかりやすい結果は「いくら儲かったか?」なのは揺るぎようがありません。だからといって過去の推移でいちばん儲かったものがこれからも儲かるか?は別の話です。
これまでの歴史の中でたくさんの偉人が株価の予想にチャレンジしてきました。その中で今の根強く残っている理論が上で紹介した統計的な手法です。上の結果からリスクσがどのように影響するかがなんとなくでもつかめれば、執筆者としてはうれしい限りです。
ここまで偉そうに書いてきましたが、僕がこの対数正規分布で株価予測をしたのは今回が初めてですw 記事やYouTube動画を作るために勉強しました。難しい難しいと思って手をつけないと理解できませんが、取り組んでみると意外に簡単なものです。対数正規分布はEXCELで関数が準備されているので、あとは株価データさえあれば数分で計算できてしまいます。チャレンジする者に優しい時代になりましたね。
ただし注意していただきたいのは、これもあくまで過去の統計値を引用しているということです。過去の統計値と違う動きをすることは想定されていません。あくまで仮定を置いて計算しやすくしている、というのを忘れないでください。妄信は厳禁です。
そうは言ってもこういう分析をされる方はそう多くありません。今回の計算から得たスキルを武器に、今後の動画を企画していこうと思います。もしご興味あればぜひチャンネル登録をよろしく!

