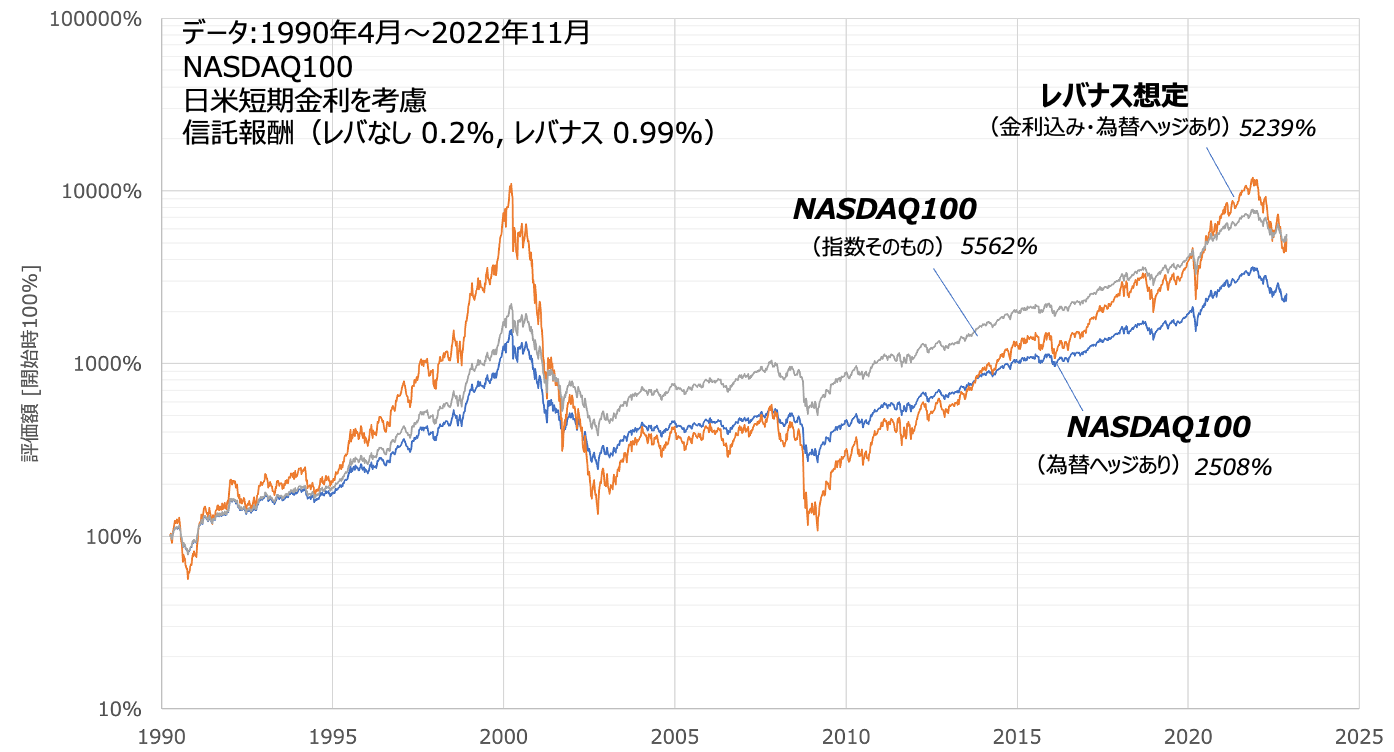
みなさん、長期投資をするにあたって重要視している概念は何でしょうか？多くの人はリターン、もしくはシャープレシオと答えることと思います。僕は後者。
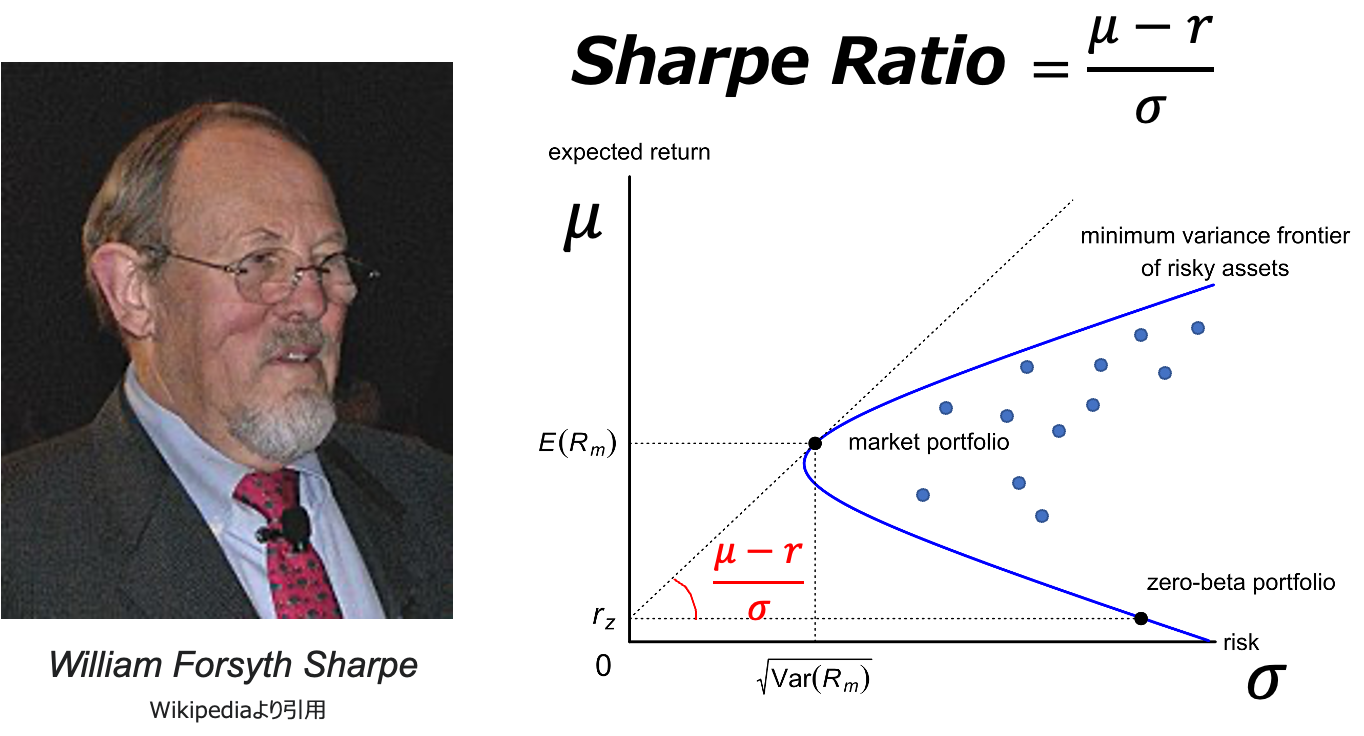
シャープレシオとはウィリアム・シャープ氏が考案したリスクあたりのリターンを示す指標で、これを最大化すること＝ムダなリスクを取らない、ということを意味します。彼はこの考えを原点にCAPMというモデルを作り上げ、ノーベル賞を受賞しました。詳しい話は以下の書籍を読むとざっくり理解できるかと思います。
僕もこのシャープレシオの考え方を信仰していて、それに沿ってS&P500にフルインベストしているわけです。なお彼の理論では市場ポートフォリオ（≒全世界に時価総額加重平均でばらまいたポートフォリオ）がシャープレシオ最大と結論づけています。
まあここまではいいんですが、自分のファイナンスに関する知識が甘く、未だに理解できていないことがあります。それが「期待収益率（リターン）」として何を使うか？というものです。
ここでは特に結論を導くつもりはないですが、どんなことを疑問におもっているか？をツラツラ書いていきます。（不躾ですがぜひ有識者の方にアドバイスいただきたいです）
とにかくこの”リターン何を使えばいいのか問題”をすっきりさせたい！その思いでいっぱいですw
※なお当方は数学に疎いので、変な表記や突拍子もないこと書いていると思います。
算術平均リターンと幾何平均リターン
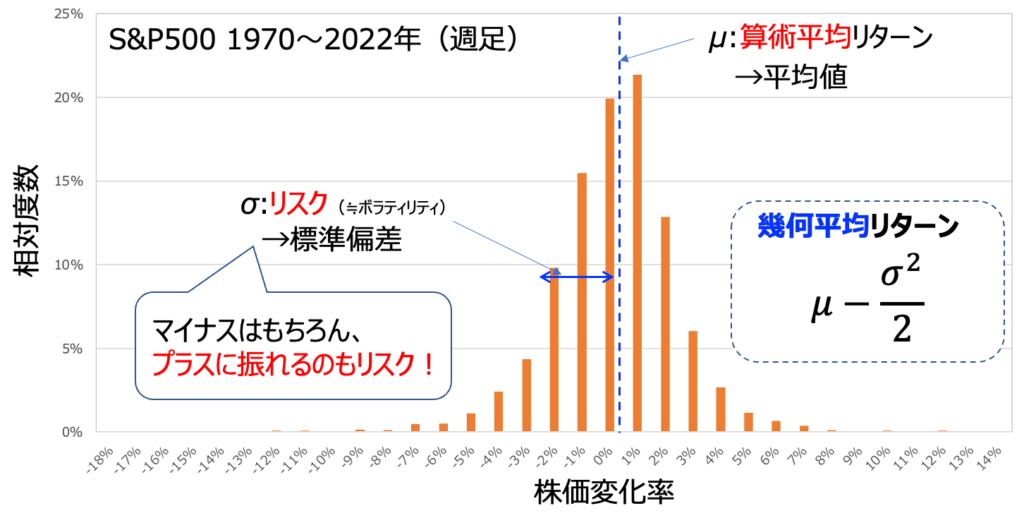
このブログでも何回か紹介していますが、リターンには大きく算術平均と幾何平均と呼ばれるものがあります。
例えば上図は週足のS&P500の株価変化をヒストグラムで整理したもので言うと、算術平均とはいわゆる”普通の”平均値です。毎週の株価変化を足し算し、その週数で割れば求まります。
一方の幾何平均リターンは、このデータをとった最初の週と最後の週の株価変化に対して”複利だとどうなる？”を率で表現したものと言っていいでしょう。つまりは週数をnとして（1+幾何平均リターン）^n を計算してやれば、実際にその株価がn週間でどれくらい成長したか？を計算できます。なお、上図のσ（標準偏差）と算術平均リターンμを使って表現された幾何平均リターンは近似式です。
実際に計算してみるとこんな感じになります。我々投資家にとって重要なのは”幾何平均リターン”だと言うのはこれでよくわかりますよね。
ここまでは幾何平均リターンと算術平均リターンのおさらい。本題はここから。
疑問：シャープレシオの計算に使用するのは？
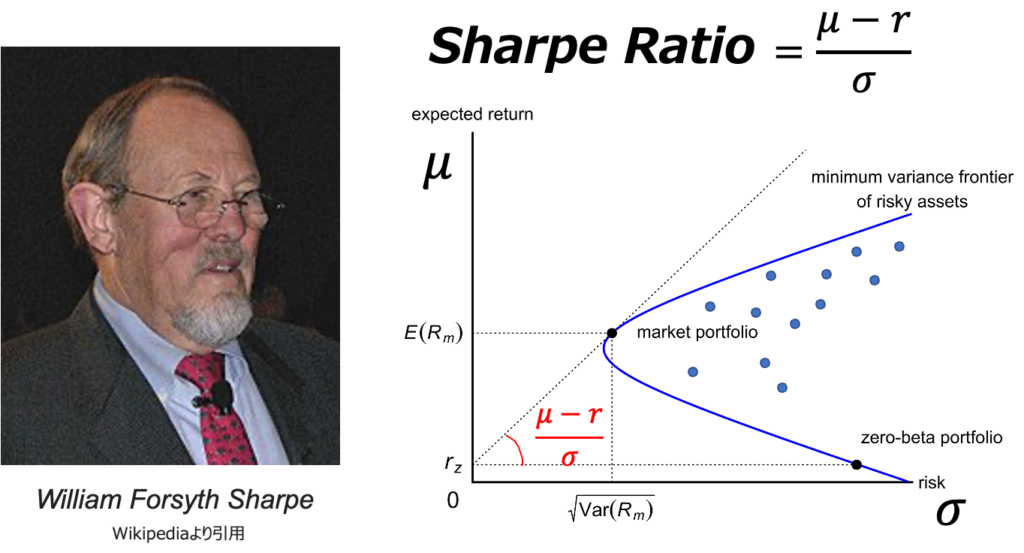
ここから僕がいつもモヤモヤとしている疑問点です。
ポートフォリオ理論などでよく登場するシャープレシオは上図のような形で表されます。rはリスクフリーレートと言って、無リスクでもらえるリターンのことです。まあ銀行預金の金利だと思えばいいかと。
この式で登場するμが前述の”幾何平均”か”算術平均”なのか？というのが疑問なのです。
文字通りにとらえると算術平均を使うのかな〜と想像できます。統計でよく使う”期待値（算術平均）”はμをよく使いますからね。実際に当ブログやYouTube内でもシャープレシオと称するものは算術平均を用いて計算してきました。
一方で前述のとおり、算術平均リターンは投資家にとって重要な指標ではありません。実際のリターンよりも過大になっていますから。これでずっともやもやしてきました。ほんとは幾何平均リターンを使うべきなんじゃない？って感じに。
調べてみると意見はいろいろあるみたい
最近、これが気になってしまって夜も眠れませんw ネット上で調べれば調べるほど、いろんな意見が出てきます。
例えばこちら。雰囲気で語って申し訳ないんですが、金融工学に詳しそうな方が自信を持って書いていらっしゃるように思えます。これはシャープレシオに「算術平均リターンを使う」前提のものです。
シャープレシオの求め方
平均リターン求め方は大変単純で、
①全部足して
②足した個数で割る
とうものであった（小学生レベル）。
〜 中略 〜
そしてリスクを求めるにはまず平均リターン５％との差の大きさをそれぞれ
1年目：３５％
2年目：３５％
3年目：３５％
4年目：３５％
と求め、その平均
(35%+35%+35%+35%)/4=35%
と計算できる。
従ってシャープレシオは、
5%/35%≒0.14
と計算できる。
この著者の方は「シャープレシオは使いもんにならない」とおっしゃっていて、それはリスクあたりの算術平均リターンだからだ！という旨で述べられております。つまりはシャープレシオは算術平均で語るもの、という理解のようです。これは今までの僕が計算してきたものと同じ解釈。
一方でこちらの少し古い記事の意見が、個人的にはすごく納得感あるものでした。
算術平均と幾何平均のトリック
そもそも、シャープレシオとは「現代ポートフォリオ理論」から派生した概念で、本来は「１期モデルにのみ適用可能な尺度」です。投資リターンの評価が１期間の場合、算術平均と幾何平均は一致しますので、バイアスのない尺度です。しかし、実証研究ではこれを複数期間の平均という形で使用しています。
もし、平均を取る段階において算術平均を採用しているならば、シャープレシオはリスク調整後リターンを過大評価していることになります。（実際のところ、算術平均を使用していることが殆どです。）
この人も相当金融工学に相当詳しそうです。おそらく「１期モデル」と呼ばれているのは、算術平均で言えばN=1の期間を対象にするという意味だと思われます。算術平均するにも１期間しかないので、どうもこうもない。
その場合には幾何平均と算術平均が一致する、というのもよくわかるのです。言わば、幾何平均リターンと算術平均リターンというのは高校生の時に習った「相加平均・相乗平均」の考え方と同じ。なので以下のような関係が成り立ちます。a1, a2・・・はその時間ステップ（例えば週とか）の株価変化だと思ってください。
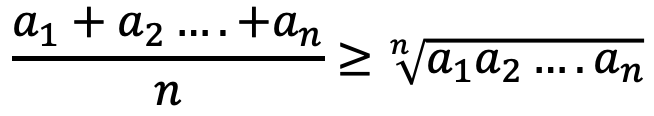
これがn=1の時を考えれば、当然両辺は a1=a1 と等号の関係になりますよね。これが恐らく上のブログの執筆者が意図している内容だと思われます。
そういうことであれば、僕のようにヒストグラムを作って複数期間データを活用していた場合には、シャープレシオは算術平均ではなく幾何平均リターンを用いた方がよさそうです。
ただ、著者の方は同時に「算術平均リターンでシャープレシオが記述されてしまっている場合が多い」とのコメントも残されており、実際世の中には混在してしまっているみたい。苦しくも自分もその一翼を担っていました。
結局どうすべきなのかは自信がありません。有識者の意見を伺いたいところですが、自分の感覚では幾何平均リターンで見るべきなのだろうと思っています。ただし、説はいろいろあるようなので、今後はシャープレシオと明記せずに「幾何平均リターン/リスク」と表現することにしようかな。それで誤解はあるまい。
※ぜひ金融工学に詳しい方メッセージ（SNS経由など）で教えていただけるとうれしいです
幾何ブラウン運動に使うμは何なのか？
もうひとついつも自信がなくなるリターンの解釈があります。それが幾何ブラウン運動モデルのμです。
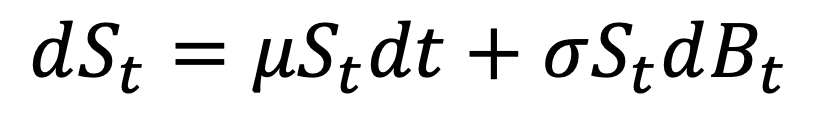
これの右辺第一項にも忌まわしいμが出てきます。Wikipediaによると以下のように説明されているものです。
定義
dSt は増分。例：金融商品の価格の変化。
dBt はブラウン運動（ウィーナー過程）の増分。
μ は（現在の St に対する割合であらわした）ドリフト。金融の場合は期待収益率。
σ は（現在の St に対する割合であらわした）ボラティリティ。
出たよ…これもまた期待収益率、と記されています。じゃあこの場合は何を使えばいいんでしょうか？
恐らく前述のシャープレシオの話のように１期間の話であれば、何を意識するでもないのでしょう。問題は複数期間を統計的に処理したときに、果たして算術平均リターンと幾何平均リターンのどちらを使うべきか？というところです。
実はこっちは確信というほどではありませんが、なんとなく自分でも理解できてる思いはあります。
仮にμがなんかしら設定されていたとして、幾何ブラウン運動の時間ステップを週毎としましょう。
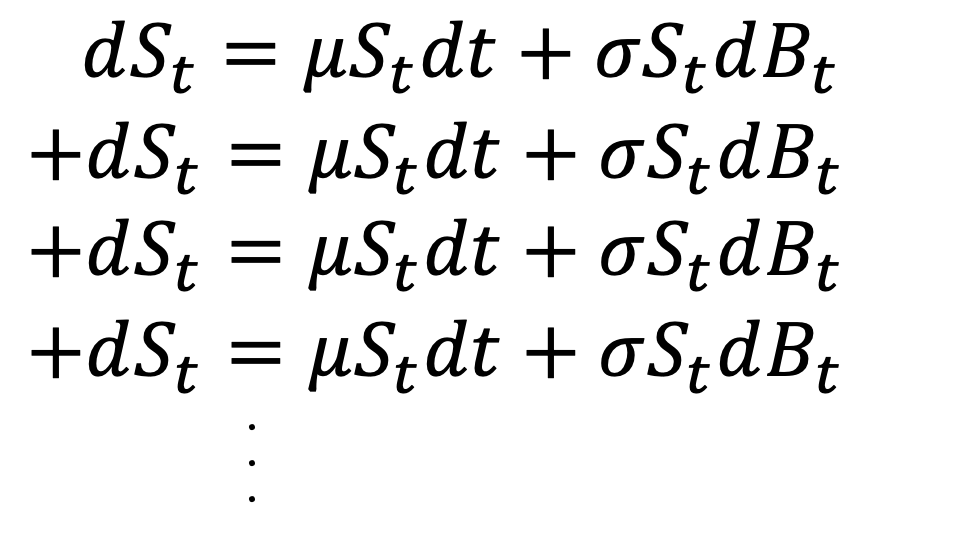
上図はイメージしやすいように幾何ブラウン運動の式を縦にたくさん並べてみました。時間ステップが週毎であれば、左辺dStは週毎の株価変化になるはずです。
そうした場合、上図のように週毎の株価変化をn週間ぶん足し合わせるのを仮想してみてください。そして両辺をnSで割れば、左辺は算術平均リターンそのものになるでしょう。※Sはその時々の株価です、手抜きですみません
一方の右辺第２項は平均値0のランダムな動きを表すものだったはずです。つまり、nを大きくとれば全部足せば0になるはず。
そうすれば右辺は第１項のみが残ることになり、それは算術平均リターンと一致する。僕はそんな理解をしていて、幾何ブラウン運動を使うときにμ、σを過去データに頼る場合はそうしています。たぶん合ってると思うんですよね…でも自信ない。この記事を見ると”幾何平均リターン”だと言ってたりするしな…
まあたぶんこの幾何ブラウン運動モデルも多期間ではなく幾何平均=算術平均とする意味で記述されているのでしょう。もし僕のように複数期間からのデータを扱う場合は算術平均が適切、いまはそういう認識です。
※・・・これも自信と確信がないので、ぜひ有識者のアドバイスいただきたいです、よろしくお願いします
追記：さっそく教えていただきました
ある論文をご紹介いただきました（ありがとうございます！）。これを見る限りは幾何ブラウン運動モデルにおいては前述の僕の解釈は間違っていなさそうです。
結論：金融工学の勉強が足りません
ぼくは１年前からYouTubeに動画投稿をするようになって、ネタ探しに苦慮した挙げ句金融工学に手を出しました。それくらいニワカです。
こういう話は教科書を読むとなんとなくスルーされてしまいがちなんですけど、いざ手を動かすと疑問が湧いたりぶち当たったりする点なんですよね。こういう時に「手を動かすって大事だな」と思いました。これらの疑問に適切に答えられない限りは本を読んでわかっていた気になっていただけなんでしょうね、実は。
ネタ探しのためで勉強をし始めましたけど、それ自体はやってよかったなと思ってます。現代ポートフォリオ理論の美しさや揺るぎない結論は、今までの自分の投資方針（インデックス全力）が裏付けられていくようで、凄く感銘を受けたものです。投資を始められた方にまず最初に知っておいてほしいくらい、すばらしいものだと思います。
そうした輪が広がっていくように、僕ももっと勉強せねばなりません。いずれ３ファクターモデルやBlack–Litterman modelも手を出したいと思ってますが、これがYouTubeで映えるイメージが全くわかないのが直近の悩みです。
おまけ：資産運用おすすめ書籍
僕が実際に読んで「ほんとうに良い本だなぁ〜」としみじみ感じた名著をご紹介します。どれもめちゃくちゃ良い本ばかり。インデックス投資を始めたての方におすすめです。
以下の中にはKindle Unlimited（月々980円 読み放題）のサービスで利用できるものもありますのでチェックしてみてください。Kindle Unlimitedは無料期間もたまにあります、いつかはわからないけど。
2024年の年初に亡くなられた山崎元さんの遺作。内容は父から息子への手紙をイメージして、資産運用や生き方のアドバイスをおくるというもの（実際に送られた手紙の内容もあります）。涙なしには読み切れない名作でした。投資における主張はいつもの著者のものと全く同じ。ブレないところが山崎さんの良さですね。ぜひ読んでもらいたい一冊。
かつて日本の長者番付で一位になったサラリーマンとして話題になった清原達郎氏の初めての著書。これまでメディアにほとんど出てこなかった氏の赤裸々な体験談が多数載せられています。内容は初心者向けではありませんが、どこにでも溢れているインデックス投資を勧めるだけの本に飽きた方にはとても面白いはず。かく言う私もその一人（笑）純粋な読み物としてとても面白いです。
これは最近複数の視聴者さんに紹介してもらって購入した本です。主張は題名どおり「余剰資金が出たら即刻インデックス投資せよ」というもので、僕も思想とほぼ一致しています。また、前半部分では「節約には限界がある」「収入を増やす努力をしよう」という主張もされていて、その辺も共感できる部分は多いです。とてもいい本だと感じましたので、よかったら手にとってみるとよいかと思います。
これは最近視聴者さんに教えてもらった本です。株式投資や資産運用の考え方を学ぶのに、とても素晴らしい名著だと思いました。著者はインデックス投資にも精通していることが伺える一方で、各個人の資産運用は人としての合理性も考慮すべきと説いてます。株式投資のリターンは「リスク（値動き）の対価」をわかりやすい例も含めて明示してくれていて、投資初心者の方にぜひ読んでみてもらいたい本ですね。
これは僕が最近読んでよかったと思ってる本です。マクロ経済における金利の重要性を懇切丁寧に説明してくれています。金利が経済の基本であることを再認識させられました。初心者でも読みやすいように書かれていて、とくに予備知識は必要ありません。投資タイミングに活かせるかと言えばそこは同意しかねますが、金利による経済の定性的な動きを理解するのはこれで十分と思いました。
米国の著名投資家ハワード・マークス氏の著書で、彼の著書はなんとあのウォーレン・バフェットのお気に入りらしいw バークシャー・ハサウェイの株主総会でこの本を配ったというウワサも残っています。ハワード・マークス氏自体はインデックス投資にも一目を置くアクティブ投資家で、市場平均に勝つのは難しいと認めつつもどうすれば勝てるか？を色々とアドバイスしてくれる本です。
僕が一番好きな本。難しい数学的な知識を必要とせず、現代ポートフォリオ理論（≒ランダムウォーク理論）をかじれます。正直な感想を言うと全ての書いてることが興味深かったわけではありません。なので隅々まで読んだわけではないですが、理論のところはとてもわかりやすいのでおすすめです。これ読んでからWikpedia見たらだいぶ理解が進みました。
上記の本に加えてもう少しファイナンスを詳しく知りたい方向けにおすすめです。CAPMの考え方やそれをもう一歩発展させた3ファクターモデルのことも理解できます。ほかにもプライシング理論やリスク管理などの基礎知識もこれで十分わかるかと。
![敗者のゲーム[原著第8版]](https://m.media-amazon.com/images/I/512Xx-NQJGL._SL160_.jpg)
インデックス投資の名著中の名著です。個人投資家にとっての投資は「ミスった者が負ける」敗者のゲームになった、というのがタイトルの由来。ここで言うミスとは、市場動向に動揺して売買してしまうことを指します。いいからインデックスホールドしとけ、という本。
インデックス投資の父でありVanguard創業者のBogle氏の名著です。僕が最も尊敬する偉人でもあります。その先見性と残された功績には尊敬の念しかありません。内容はインデックス投資のベーシックな内容ですが、後半には債券との組み合わせ論などにも言及されています。全部が全部同意見というわけではありませんが、インデックス投資を志す者であれば必読書とも言ってよいかと。
ランダムウォーク理論（株価の動きはわからないという前提を置く理論）について、歴史を交えて語った本。これも名著と言われています。理論の概念はざっくりとわかるかと。歴史の部分が長くて、そこは読み飛ばしました。
本をほとんど読まない僕が唯一知ってる作家さん、橘玲さんの本。とても読みやすい文章で書かれていて、こんな文が書きたいなといつも思ってます。僕が海外株を中心に買っているのはこの本の考え方に近いです。
この本は僕が初めて読んだ投資関連の書籍。当時、個別株で失敗し、偶然思うがままに買い付けた米国株インデックスETFに出会い、それにいい感触をもっていました。その感触を自信に変えてくれた本です。
※以下のリンク先におすすめ書籍をまとめています
