みなさん、レバレッジ投信は保有してますか?僕は最近の流行りに乗ってレバナスに少し手を出して案の定火傷していますw 今のポートフォリオ上は5%程度の比率です。

このレバナスはSNS上などでも注目度が高くて、様々な論争を生んでいます。その論争には顔を出したくないのですが、注目度の高いテーマは動画再生数もとれるというのも事実です。なので、できる限りフラットな視点で今回もレバナスを分析してみたいと思います。テーマは「レバナスの危険性」です。
国が非課税口座にレバレッジ商品を認めない方針を打ち出したりしたのもきっかけで、レバ投信は危険だと言われることが多くなりました。まあ実際に投資されている方はそんなことは重々承知だと思います。しかしどれくらい危険か?とか、なぜ危険と言われるかはあまり理解されていないんじゃないでしょうか?今回は投資の素人目線からその危険性について僕なりに考察してみたいと思います。この記事がこれからレバナスに投資してみようと思う方の参考になれば、それ以上にうれしいことはありません。
YouTubeも見てね!
幾何ブラウン運動モデルを使います
このブログや動画を以前から見ていただいている方にはお馴染みの手法ですが、今回もランダムウォーク理論(幾何ブラウン運動モデル)を使って分析を進めていきます。概念は以下の書籍を読むとだいたいわかるので、この名著たちに任せることにしましょう。
平たく言えば「株価は規則性なく動く」と仮定するものです。日々の株価変化率は正規分布とするとみなします。例えば、NASDAQ100の実際の動きと正規分布でしてみたのが以下のグラフです。※今回はレバナスがテーマなのでNASDAQ100で議論を進めます。
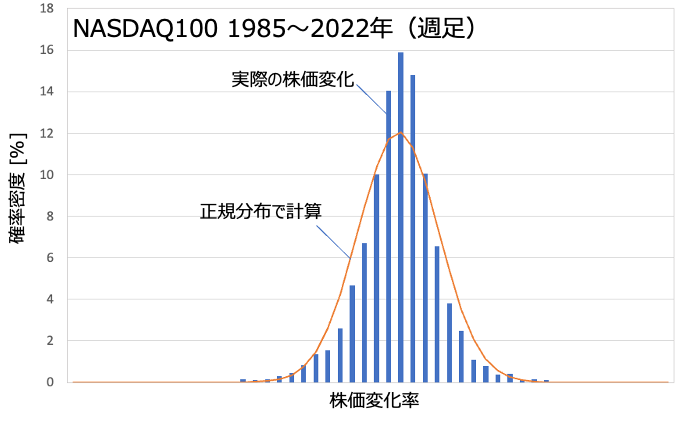
まあそれなりには表現できていると思います。完璧ではありませんが、非常に簡素なモデルでここまで表現できれば十分でしょう。実際の株価は平均値付近により固まっていて、裾野の端っこにも分布(ロングテールとも言う)してるような印象です。

実際の幾何ブラウン運動モデルを使った計算例を見ていきましょう。横軸の規格化した評価額は元本を1と表現した数値です。つまり、1未満の領域は元本割れを意味します。縦軸の確率密度は、用語で言うと堅苦しいですが、どれくらいの確率でそこにいるか?を示したものだと思ってください。
実際のNASDAQ100(37年間)の推移を見てみると、やや中央値(50%の確率でそのリターンを上回る/下回るしきい値)よりやや下あたりにきています。これで何を言うわけではありませんが、幾何ブラウン運動モデルによってこんな感じで将来の株価を確率で表現できるのです。
今回は「レバナスの危険性」について考えたいので、このモデルを使って「元本割れ確率」を計算していきます。
レバレッジによって元本割れ確率はどうなるのか?
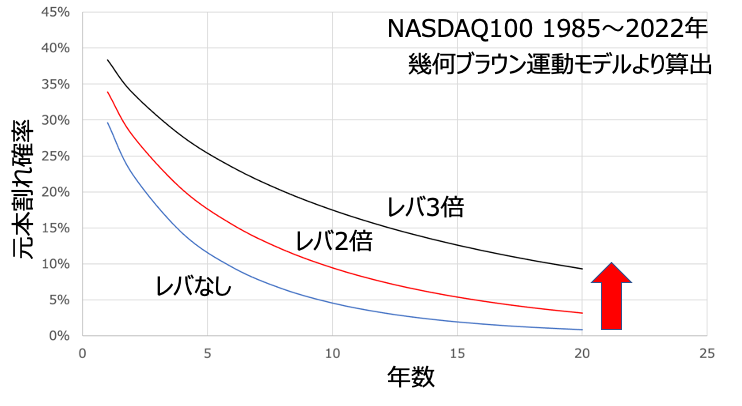
上図は横軸に運用年数、縦軸に元本割れ確率をレバレッジ倍数ごとにプロットしたものです。どれも年数を経ると長期投資の旨味が出てきて元本割れ確率は右肩下がりに推移します。これ自体はいいことですが、レバレッジをかけたほうが元本割れする確率は上昇しているのが明らかです。そしてレバなしとレバ2倍の上昇具合に比べて、レバ3倍にしたときの上昇幅がシャレになっていません。どうやら、倍数を上げていくと飛躍的に元本割れ確率が上がっていそうです。
ただ上のグラフはテキトーにレバ倍数を選んできたものです。どこかに元本割れ確率が下がる、ちょうどいいレバ倍数があったりしないのでしょうか?
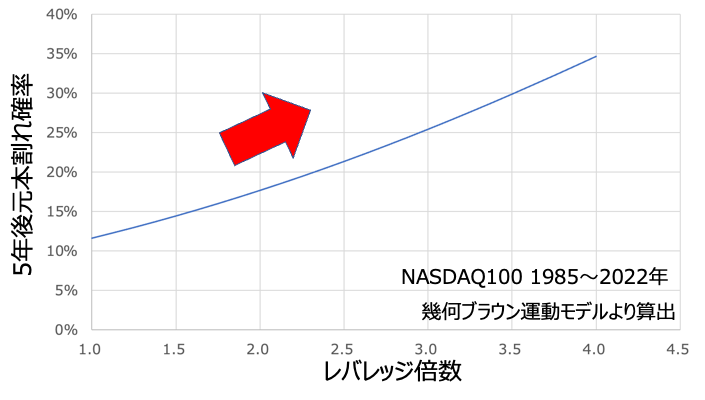
上のグラフはレバ倍数を横軸に、5年後の元本割れ確率をプロットしたものです。これを見る限りはレバ倍数1以上の領域で元本割れ確率を下げることはできなさそう。レバレッジをかける限り元本割れ確率は単調増加です。
元本割れ確率を下げるレバレッジはないのか?
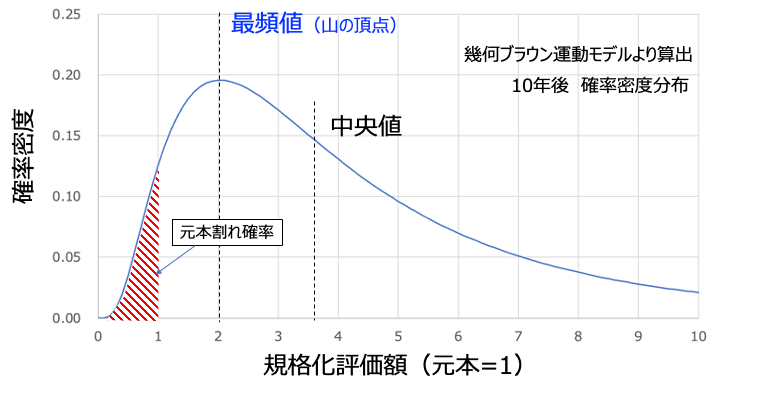
上の図はNASDAQ100(1985〜2022)までのデータをもとに幾何ブラウン運動モデルにて10年後株価の確率密度分布を計算したものです。分布というものには色々な特性値があるのですが、僕が注目したのは最頻値。これは山の頂点の位置を意味します。元本割れ確率は上図の赤いハッチング領域ですから、この最頻値が最大になればこの面積が最小になるのでは?と考えたわけです。
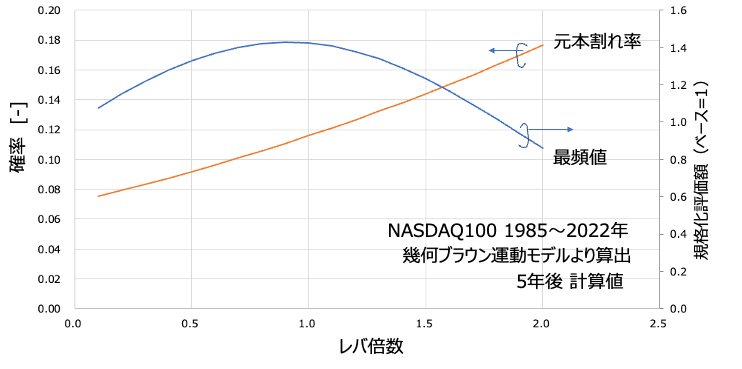
実際に最頻値と元本割れ確率をレバ倍数を横軸にプロットしてみました。今回は最頻値の最大値が見えるようにレバ倍数1以下もプロットしています。するとどうでしょうか?最頻値の最大値は0.9倍付近にあるのですが、そんなものは何も関係ない動きで元本割れ率はレバ倍数に対して単調増加傾向を維持しています。0.9倍以下で元本割れ確率が上がるのかな?と思ってましたが、全くそんなことはありません。レバをかければかけるほど元本割れ確率はあがっていくというのが真理のようです。まあ最頻値はただ単に”いちばん人が多いところ”という意味しかありません。時間経過とともに平ぺったくなる対数正規分布において、時間が経てば無意味な指標になっていくということなんでしょう。
上記は数学的に証明したわけではありませんが、どうやらそんな結論が導けそうな気はします。近々チャレンジしてみようとは思いますが、需要がなさそうなのでお蔵入りするかも。
レバをかけると良くなる部分もある

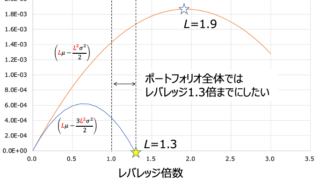
レバをかけると元本割れ率が上がるだけであれば全くいいことはありません。しかし、リターンの中央値を見れば、レバをかける意味が見えてきます。
NASDAQ100の場合、上図のようにレバレッジ2.7倍までは中央値が上がるような特性を持っています。もちろん元本割れ率はそれに応じて上がってますね。つまりは防御力を削って攻撃力を上げる行為が、この領域でのレバレッジをかけるということなのです。
そして2.7倍を超えるレバレッジは攻撃力も下がっていきます。これらの商品は短期投資においてのみ使うべきものだと言っていいでしょう。たぶん。

ここで確率密度分布に立ち返って、レバレッジをかけたときの分布の違いを見てみます。まず最初に見てわかるのがレバレッジをかけると分布のトップ(最頻値)が左に移動していることでしょう。これは大損する人が増えていくことを意味しています。
一方で中央値が上がっていくレバ2倍付近までは山の”高さ”が下がっていってるのもわかります。これは最頻値にいる人数が減って、右の大儲けする人が増えてるとも言えるんですよね。これが中央値を上げる動きにつながっているものと思われます。
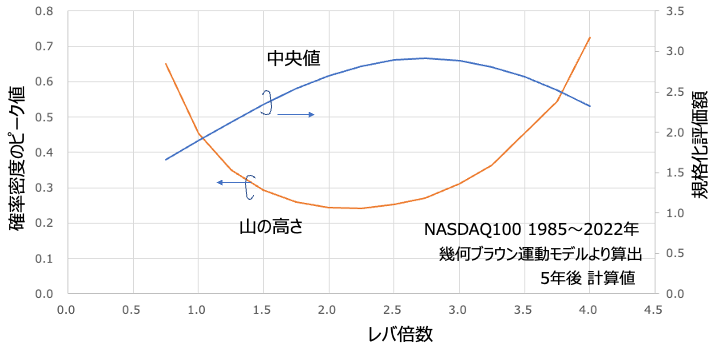
実際に中央値と山の高さをプロットしたのが上の図です。上記の仮説が正しければ中央値がピークになるレバ倍数で山の高さが最低になるはずですが、ちょっとずれてますね。なので、中央値だけではなく、他の要素も色々からみあって山の高さが低くなっているみたい。その原因はめんどくさいので後日考えますw
過去の実際の動きと比べてみたらどう?

最近は他のYouTuberさんとの差別化をねらってあまり過去チャートとの比較はやらないようにしています。N=1で確率を議論しているようなものを見ると、ちょっとどうかしてると思うし、同レベルだと思われたくない気持ちがあるからです。しかし、過去に起こったという事実には非常に説得力があります。なので、今回の検討を過去データと比較してみることにしましょう。まああれだ、アテにしないでねw
上図はレバ倍数を横軸にとって、縦にレバなしの評価額を1とした場合の評価額をプロットしたものです。実際のNASDAQ100と今回計算したモデルでの中央値をプロットしてみました。
これを見ると、リターンがMAXになるレバ倍数は中央値MAXよりもちょっと小さいところにいるのがわかります。ただ、かなりいい線をついてるのはわかるかと。

上図は実際にレバ倍数ごとに株価推移を計算してみたものです。たしかにレバ2.5倍付近まではいい感じにリターンが増えてます。レバ倍数を上げすぎると暴落時に下がりすぎて戻ってこない現象もよくわかるかと。これがいわゆる逓減ですね。
ここで紹介した結果はあくまでN=1の議論です。結果のご判断はお任せしますが、過信はしないように。
結論:レバをかける以上は元本割れ率UPは覚悟しろ
この記事内ではNASDAQ100のデータを使えるだけ全部使いました。もしもっと安全目の試算をする場合は、以下の表の「安全重視」の計算結果を引用してください。これはITバブル直前からのデータを使っているので、かなり悲観的な計算になっています。

この表が以上の結果を踏まえた僕の考えです。以前の記事で「最頻値が時間とともに左に動かない」ことがいいんじゃない?と提言しましたが、それは元本割れ確率で論ずる限りは気分の問題だったようです。まあそれでも長期運用すればするほど最頻値が下がるのは、なんだか気持ちわるいですよね・・・。
そして今回の計算でわかったのはレバをかける限りはどうやっても元本割れ確率は上がるということ。さらにはある倍数までは中央値を大きくできるということです。つまり、その倍数以下の領域なら、レバ倍数によって防御力と攻撃力をカスタムできると言っていいでしょう。まあどこまでやるかはどこまで攻めるかにお任せします。
とは言え、最も重要なのは「リスク許容」だと言うのを忘れてはいけません。
YouTubeも見てね!
楽天証券ユーザーならまずは「楽天モバイル」
-
3GB未満なら税抜880円/月、使いすぎても上限2880円/月のわかりやすいプランが良い。
-
楽天市場のSPUは驚異の+4倍!僕はざくざくポイント貯めて、クレカ積立で消化してます。
-
回線も強化されてきて、圏外になることもほとんどなくなってます。
今から投資始める方におすすめの証券会社
-
僕の主力 楽天・プラス・S&P500 や人気の楽天SCHD が買える唯一の証券会社。
-
とにかく視認性がよくて使いやすいのが最大の魅力。
-
楽天プラスシリーズは保有するだけで楽天ポイントもらえる。
- 公式:https://kabu.com/
- au Payカードと組合せての積立で0.5%ポイント還元。
- 公式:https://www.matsui.co.jp/
- 投信信託を持ってるだけでポイントもらえる投信残高ポイントに強い
- 公式サイト:https://www.sbisec.co.jp/
- SBI独自の四半期決算型の高配当投資信託を購入できる唯一の証券会社
- 投資信託で高配当を楽しみたい方はSBI証券が良いでしょう。
証券口座乗っ取り対策に!パスワード管理は1Passwordで
- 公式:https://1password.com/jp
- どんな端末を使っていてもストレスなく使えるパスワードアプリ
- 強固なセキュリティ、過去に重大漏洩事故は起こっていない安心感
投資を学ぶなら:資産運用ですごく勉強になる書籍
僕が実際に読んで「ほんとうに良い本だなぁ〜」としみじみ感じた名著をご紹介します。どれもめちゃくちゃ良い本ばかり。インデックス投資を始めたての方におすすめです。
以下の中にはKindle Unlimited(月々980円 読み放題、初めてだと30日無料キャンペーンもある)のサービスで利用できるものもありますのでチェックしてみてください。
この本は僕が初めて読んだ投資関連の書籍。当時、個別株で失敗し、偶然思うがままに買い付けた米国株インデックスETFに出会い、それにいい感触をもっていました。その感触を自信に変えてくれた本です。僕と同じく、初めて投資書籍を読まれる方にはこの本を最初にオススメします。
投資に関するネット記事は数あれど、最も有名で価値ある記事はコレなのでは?という記事の書籍版です。ぜひ投資書籍の2冊目に読んでほしい一冊としてピックアップしました。これを読むだけで本当に資産運用が完結する内容になっていて、僕も当時衝撃を受けました。もちろん書籍版の内容の本質はネット記事とほぼ同じですが、理論編がわかりやすく改定されていたり、読みやすくなっています。
インデックス投資の名著中の名著です。個人投資家にとっての投資は「ミスった者が負ける」敗者のゲームになった、というのがタイトルの由来。ここで言うミスとは、市場動向に動揺して売買してしまうことを指します。いいからインデックスホールドしとけ、という本。インデックス投資家の教養として読むべき本です。
これは僕が最近読んでよかったと思ってる本です。マクロ経済における金利の重要性を懇切丁寧に説明してくれています。金利が経済の基本であることを再認識させられました。初心者でも読みやすいように書かれていて、とくに予備知識は必要ありません。投資タイミングに活かせるかと言えばそこは同意しかねますが、金利による経済の定性的な動きを理解するのはこれで十分と思いました。
この本はKindle Unlimitedの読み放題サービスで提供されていることが多いです。Kindle Unlimitedは初めてであれば30日無料体験が使えるので、それで読み切ってしまうのもいいかと思います。僕はそうしました。
これは最近複数の視聴者さんに紹介してもらって購入した本です。主張は題名どおり「余剰資金が出たら即刻インデックス投資せよ」というもので、僕も思想とほぼ一致しています。また、前半部分では「節約には限界がある」「収入を増やす努力をしよう」という主張もされていて、その辺も共感できる部分は多いです。とてもいい本だと感じましたので、よかったら手にとってみるとよいかと思います。
これは最近視聴者さんに教えてもらった本です。株式投資や資産運用の考え方を学ぶのに、とても素晴らしい名著だと思いました。著者はインデックス投資にも精通していることが伺える一方で、各個人の資産運用は人としての合理性も考慮すべきと説いてます。株式投資のリターンは「リスク(値動き)の対価」をわかりやすい例も含めて明示してくれていて、投資初心者の方にぜひ読んでみてもらいたい本ですね。
2024年の年初に亡くなられた山崎元さんの遺作。内容は父から息子への手紙をイメージして、資産運用や生き方のアドバイスをおくるというもの(実際に送られた手紙の内容もあります)。涙なしには読み切れない名作でした。投資における主張はいつもの著者のものと全く同じ。ブレないところが山崎さんの良さですね。ぜひ読んでもらいたい一冊。
米国の著名投資家ハワード・マークス氏の著書で、彼の著書はなんとあのウォーレン・バフェットのお気に入りらしいw バークシャー・ハサウェイの株主総会でこの本を配ったというウワサも残っています。ハワード・マークス氏自体はインデックス投資にも一目を置くアクティブ投資家で、市場平均に勝つのは難しいと認めつつもどうすれば勝てるか?を色々とアドバイスしてくれる本です。
僕が一番好きな本。難しい数学的な知識を必要とせず、現代ポートフォリオ理論(≒ランダムウォーク理論)をかじれます。正直な感想を言うと全ての書いてることが興味深かったわけではありません。なので隅々まで読んだわけではないですが、理論のところはとてもわかりやすいのでおすすめです。これ読んでからWikpedia見たらだいぶ理解が進みました。
上記の本に加えてもう少しファイナンスを詳しく知りたい方向けにおすすめです。CAPMの考え方やそれをもう一歩発展させた3ファクターモデルのことも理解できます。ほかにもプライシング理論やリスク管理などの基礎知識もこれで十分わかるかと。
インデックス投資の父でありVanguard創業者のBogle氏の名著です。僕が最も尊敬する偉人でもあります。その先見性と残された功績には尊敬の念しかありません。内容はインデックス投資のベーシックな内容ですが、後半には債券との組み合わせ論などにも言及されています。全部が全部同意見というわけではありませんが、インデックス投資を志す者であれば必読書とも言ってよいかと。
ランダムウォーク理論(株価の動きはわからないという前提を置く理論)について、歴史を交えて語った本。これも名著と言われています。理論の概念はざっくりとわかるかと。歴史の部分が長くて、そこは読み飛ばしました。
本をほとんど読まない僕が唯一知ってる作家さん、橘玲さんの本。とても読みやすい文章で書かれていて、こんな文が書きたいなといつも思ってます。僕が海外株を中心に買っているのはこの本の考え方に近いです。
かつて日本の長者番付で一位になったサラリーマンとして話題になった清原達郎氏の初めての著書。これまでメディアにほとんど出てこなかった氏の赤裸々な体験談が多数載せられています。内容は初心者向けではありませんが、どこにでも溢れているインデックス投資を勧めるだけの本に飽きた方にはとても面白いはず。かく言う私もその一人(笑)純粋な読み物としてとても面白いです。
社会保険料がホットな話題として挙げられることが増えました。本書はその社会保険料の節約として最も有名な「マイクロ法人スキーム」のきっかけになった名著です。いま巷で使われているマイクロ法人という言葉は、この書籍で初めて使われたと言われています。もしマイクロ法人設立に興味があれば、まずは最初のバイブルとして読破しておくべき一冊です。
※以下のリンク先におすすめ書籍をまとめています




![敗者のゲーム[原著第8版]](https://m.media-amazon.com/images/I/512Xx-NQJGL._SL160_.jpg)